
已知数列 的前
的前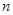 项和
项和 ,数列
,数列 满足
满足
 .
.
(Ⅰ)求数列 的通项
的通项 ;(Ⅱ)求数列
;(Ⅱ)求数列 的通项
的通项 ;
;
(Ⅲ)若 ,求数列
,求数列 的前
的前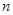 项和
项和 .
.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)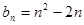 ;(Ⅲ)
;(Ⅲ)
解析试题分析:(Ⅰ)由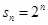 ,得当
,得当 时,
时, ,当
,当 时,
时, ,不满足
,不满足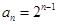 ,因此所求
,因此所求 .
.
(Ⅱ)由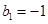 ,
,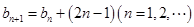 ,可得递推公式
,可得递推公式 ,所以
,所以 ,
,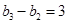 ,
, , ,
, , ,将上列各式两边累加可得
,将上列各式两边累加可得 ,再根据等差数列前
,再根据等差数列前 项和公式可求得
项和公式可求得 (叠加消项法在求数列的通项、前
(叠加消项法在求数列的通项、前 项和中常常用到,其特点是根据等式两边结构特征,一边相加可消掉中间项,另一边相加可以得到某一特殊数列或是常数).
项和中常常用到,其特点是根据等式两边结构特征,一边相加可消掉中间项,另一边相加可以得到某一特殊数列或是常数).
(Ⅲ)由题意得当 时,
时, ,当
,当 时,
时, ,所以所求
,所以所求 ,
, ,
,
将两式相减得 ,
,
从而可求得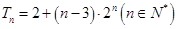 (错位相减法是求数列前项
(错位相减法是求数列前项 和的常用方法,它适用于如果一个数列的各项是由一个等差数列和一个等比数列的对应各项之积构成的).
和的常用方法,它适用于如果一个数列的各项是由一个等差数列和一个等比数列的对应各项之积构成的).
试题解析:(Ⅰ)∵ ,
,
∴ . 2分
. 2分
∴ . 3分
. 3分
当 时,
时, ,
,
∴ 4分
4分
(Ⅱ)∵
∴ ,
, ,
, ,
, ,
,
以上各式相加得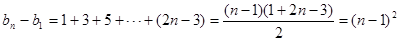 .
.
∵ ,
,
∴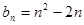 . 9分
. 9分
(Ⅲ)由题意得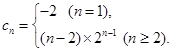
∴ ,
,
∴ ,
,
∴

= ,
,
∴ . 13分
. 13分
考点:数列通项公式,错位相减法求和.


科目:高中数学 来源: 题型:解答题
已知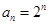 ,把数列
,把数列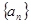 的各项排成如图所示的三角形状,记
的各项排成如图所示的三角形状,记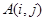 表示第i行中第j个数,则结论
表示第i行中第j个数,则结论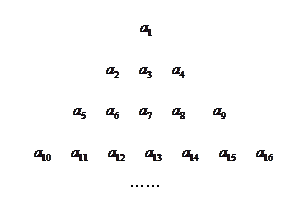
①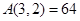 ;
;
②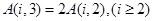 ;
;
③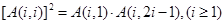 ;
;
④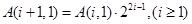 .
.
其中正确的是__________ (写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知集合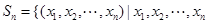 是正整数
是正整数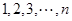 的一个排列
的一个排列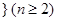 ,函数
,函数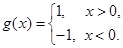 对于
对于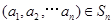 ,定义:
,定义: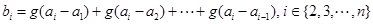 ,
,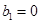 ,称
,称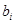 为
为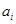 的满意指数.排列
的满意指数.排列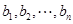 为排列
为排列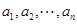 的生成列.
的生成列.
(Ⅰ)当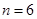 时,写出排列
时,写出排列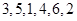 的生成列;
的生成列;
(Ⅱ)证明:若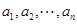 和
和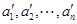 为
为 中两个不同排列,则它们的生成列也不同;
中两个不同排列,则它们的生成列也不同;
(Ⅲ)对于 中的排列
中的排列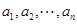 ,进行如下操作:将排列
,进行如下操作:将排列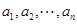 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加
从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com