
已知集合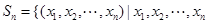 是正整数
是正整数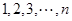 的一个排列
的一个排列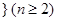 ,函数
,函数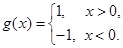 对于
对于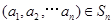 ,定义:
,定义: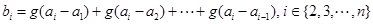 ,
,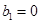 ,称
,称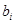 为
为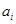 的满意指数.排列
的满意指数.排列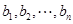 为排列
为排列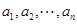 的生成列.
的生成列.
(Ⅰ)当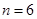 时,写出排列
时,写出排列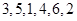 的生成列;
的生成列;
(Ⅱ)证明:若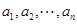 和
和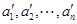 为
为 中两个不同排列,则它们的生成列也不同;
中两个不同排列,则它们的生成列也不同;
(Ⅲ)对于 中的排列
中的排列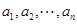 ,进行如下操作:将排列
,进行如下操作:将排列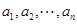 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加
从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加 .
.
(I) ;(Ⅱ)详见解析;(Ⅲ)详见解析.
;(Ⅱ)详见解析;(Ⅲ)详见解析.
解析试题分析:弄懂已知条件“对于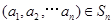 ,定义:
,定义: ,
,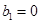 ,称
,称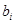 为
为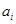 的满意指数.”是解题的关键;把握第(I)问,由特殊到一般,才能顺利求(II)(III).
的满意指数.”是解题的关键;把握第(I)问,由特殊到一般,才能顺利求(II)(III).
试题解析:(Ⅰ)解:当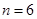 时,排列
时,排列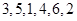 的生成列为
的生成列为 . 3分
. 3分
(Ⅱ)证明:设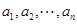 的生成列是
的生成列是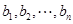 ;
;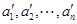 的生成列是与
的生成列是与 .
.
从右往左数,设排列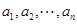 与
与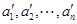 第一个不同的项为
第一个不同的项为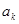 与
与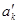 ,即:
,即: ,
, ,
, ,
, ,
,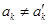 .
.
显然  ,
, ,
, ,
, ,下面证明:
,下面证明: . 5分
. 5分
由满意指数的定义知,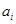 的满意指数为排列
的满意指数为排列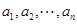 中前
中前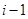 项中比
项中比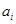 小的项的个数减去比
小的项的个数减去比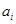 大的项的个数.由于排列
大的项的个数.由于排列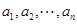 的前
的前 项各不相同,设这
项各不相同,设这 项中有
项中有 项比
项比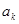 小,则有
小,则有 项比
项比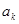 大,从而
大,从而 .
.
同理,设排列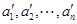 中有
中有 项比
项比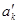 小,则有
小,则有 项比
项比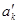 大,从而
大,从而 .
.
因为 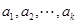 与
与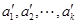 是
是 个不同数的两个不同排列,且
个不同数的两个不同排列,且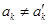 ,所以
,所以  , 从而
, 从而  . 所以排列
. 所以排列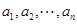 和
和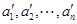 的生成列也不同. 8分
的生成列也不同. 8分
(Ⅲ)证明:设排列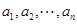 的生成列为
的生成列为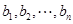 ,且
,且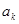 为
为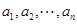 中从左至右第一个满意指数为负数的项,所以
中从左至右第一个满意指数为负数的项,所以  . 9分
. 9分
依题意进行操作,排列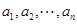 变为排列
变为排列 ,设该排列的生成列为
,设该排列的生成列为 . 10分
. 10分
所以 


 .
.
所以,新排列的各项满意指数之和比原排列的各项满意指数之和至少增加 . &nb
. &nb


科目:高中数学 来源: 题型:解答题
(本小题13分) 已知数列{a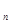 }满足0<a
}满足0<a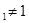 , 且
, 且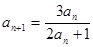 (n
(n N*).
N*).
(1) 求证:an+1≠an;
(2) 令a1=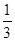 ,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.
,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com