
已知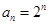 ,把数列
,把数列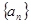 的各项排成如图所示的三角形状,记
的各项排成如图所示的三角形状,记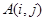 表示第i行中第j个数,则结论
表示第i行中第j个数,则结论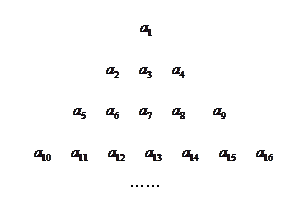
①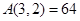 ;
;
②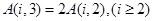 ;
;
③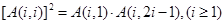 ;
;
④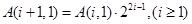 .
.
其中正确的是__________ (写出所有正确结论的序号).
①②③④
解析试题分析:观察三角形中第i行最后一个数的下脚标,得知下脚标值是该行的行数的平方,从而得到A(i,j)的表达式,再依次分析,①A(2,3)=a4=24=16;即①正确;
由图可知,第i行最后一个数是ai2,
∴②A(i,3)=a(i-1)2+3=2i2-2i+4,A(i,2)=a(i-1)2+2=2i2-2i+3
∴A(i,3)=2A(i,2)(i≥2);即②正确;
③[A(i,i)]2=(a(i-1)2+i)2=(2i2-i+1)2
A(i,1)•A(i,2i-1)=2i2-2i+2•2i2=22(i2-i+1)=(2i2-i+1)2=[A(i,i)]2,即③正确;
④A(i+1,1)=ai2+1=2i2+1,A(i,1)•22i-1=2i2-2i+2•22i-1=2i2+1
∴A(i+1,1)=A(i,1)•22i-1,即④正确;
故答案为:①②③④.
考点:本试题主要考查了数列最一般的方法是观察法。
点评:解决该试题的关键是通过行数与项之间的关系可以找到规律,题中还反映了从特殊到一般的数学思想.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com