
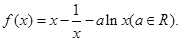
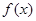 的单调性;
的单调性;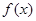 有两个极值点
有两个极值点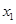 和
和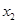 ,记过点
,记过点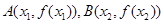 的直线的斜率为
的直线的斜率为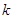 ,问:是否存在
,问:是否存在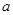 ,使得
,使得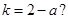 若存在,求出
若存在,求出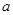 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.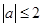 时
时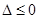 ,
,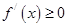 故
故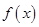 在
在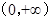 上单调递增 ;
上单调递增 ;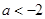 时
时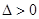 ,
,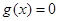 的两根都小于
的两根都小于 ,在
,在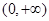 上,
上,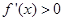 ,
,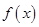 在
在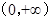 上单调递增;
上单调递增;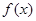 分别在
分别在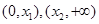 上单调递增,在
上单调递增,在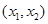 上单调递减.
上单调递减.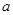 ,使得
,使得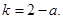
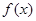 的定义域为
的定义域为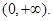
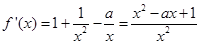 1分
1分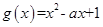 ,其判别式
,其判别式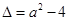 2分
2分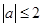 时
时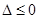 ,
,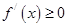 故
故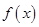 在
在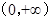 上单调递增 3分
上单调递增 3分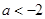 时
时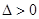 ,
,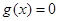 的两根都小于
的两根都小于 ,在
,在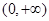 上,
上,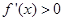 ,
,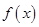 在
在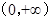 上单调递增 4分
上单调递增 4分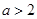 时
时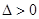 ,
,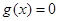 的两根为
的两根为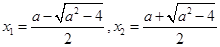 ,
,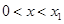 时,
时, 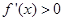 ;当
;当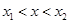 时,
时, 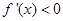 ;当
;当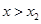 时,
时, 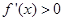 ,故
,故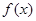 分别在
分别在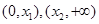 上单调递增,在
上单调递增,在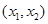 上单调递减. 6分
上单调递减. 6分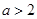 .因为
.因为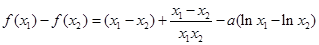 ,
,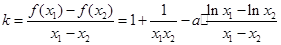 7分
7分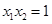 .于是
.于是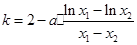 8分
8分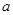 ,使得
,使得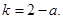 则
则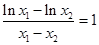 .即
.即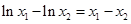 . 9分
. 9分 0分
0分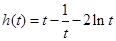 在
在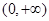 上单调递增, 11分
上单调递增, 11分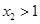 ,所以
,所以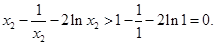 这与
这与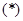 式矛盾.
式矛盾.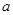 ,使得
,使得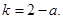 12分
12分

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com