
【题目】某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30 ![]() nmile,CD=250
nmile,CD=250 ![]() nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ= .
nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ= . 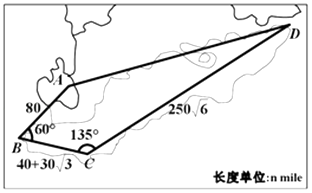
科目:高中数学 来源: 题型:
【题目】已知直线l在直角坐标系xOy中的参数方程为 ![]() 为参数,θ为倾斜角),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,在极坐标系中,曲线的方程为ρ﹣ρcos2θ﹣4cosθ=0.
为参数,θ为倾斜角),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,在极坐标系中,曲线的方程为ρ﹣ρcos2θ﹣4cosθ=0.
(1)写出曲线C的直角坐标方程;
(2)点Q(a,0),若直线l与曲线C交于A、B两点,求使 ![]() 为定值的值.
为定值的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axlnx+bx(a≠0)在(1,f(1))处的切线与x轴平行,(e=2.71828)
(1)试讨论f(x)在(0,+∞)上的单调性;
(2)①设g(x)=x+ ![]() ,x∈(0,+∞),求g(x)的最小值; ②证明:
,x∈(0,+∞),求g(x)的最小值; ②证明: ![]() ≥1﹣x.
≥1﹣x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy 中,F,A,B 分别为椭圆 ![]() 的右焦点、右顶点和上顶点,若
的右焦点、右顶点和上顶点,若 ![]()
(1)求a的值;
(2)过点P(0,2)作直线l 交椭圆于M,N 两点,过M 作平行于x 轴的直线交椭圆于另外一点Q,连接NQ ,求证:直线NQ 经过一个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出n瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这n瓶酒,并重新按品质优劣为它们排序,这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分. 现设n=4,分别以a1 , a2 , a3 , a4表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令X=|1﹣a1|+|2﹣a2|+|3﹣a3|+|4﹣a4|,
则X是对两次排序的偏离程度的一种描述.
(Ⅰ)写出X的可能值集合;
(Ⅱ)假设a1 , a2 , a3 , a4等可能地为1,2,3,4的各种排列,求X的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有X≤2,
①试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);②你认为该品酒师的酒味鉴别功能如何?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂每日生产一种大型产品2件,每件产品的投入成本为1000元.产品质量为一等品的概率为0.5,二等品的概率为0.4,每件一等品的出厂价为5000元,每件二等品的出厂价为4000元,若产品质量不能达到一等品或二等品,除成本不能收回外,每生产1件产品还会带来1000元的损失.
(Ⅰ)求在连续生产的3天中,恰有两天生产的2件产品都为一等品的概率;
(Ⅱ)已知该厂某日生产的这种大型产品2件中有1件为一等品,求另1件也为一等品的概率;
(Ⅲ)求该厂每日生产这种产品所获利润ξ(元)的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com