
(本小题满分10分)选修4-1:几何证明选讲
如图,在 中,
中, ,以
,以 为直径的圆
为直径的圆 交
交 于点
于点 ,点
,点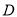 是
是 边的中点,连接
边的中点,连接 交圆
交圆 于点
于点 .
.

(Ⅰ)求证: 是圆
是圆 的切线;
的切线;
(Ⅱ)求证: .
.
【答案】(1)证明详见解析;(2)证明详见解析.
【解析】
试题分析:本题主要考查圆的基本性质等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用三角形中的角的相等关系, ,
, ,
,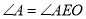 ,证明
,证明 和
和 为全等三角形,得直角存在,进而证明
为全等三角形,得直角存在,进而证明 是圆
是圆 的切线;第二问,利用切线长定理和切割线定理,建立关联等式,并化简即可证明.
的切线;第二问,利用切线长定理和切割线定理,建立关联等式,并化简即可证明.
试题解析:(Ⅰ)连结 .∵点
.∵点 是
是 中点,点
中点,点 是
是 中点,
中点,
∴ ,∴
,∴ ,
, .
.
∵ ,∴
,∴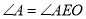 ,∴
,∴ .
.
在 和
和 中,∵
中,∵ ,
, ,
,
∴ ,即
,即 .
.
∵ 是圆
是圆 上一点,∴
上一点,∴ 是圆
是圆 的切线.
的切线.
(Ⅱ)延长 交圆
交圆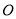 于点
于点 .∵
.∵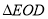 ≌
≌ ,∴
,∴ .
.
∵点 是
是 的中点,∴
的中点,∴ .
.
∵ 是圆
是圆 的切线,∴
的切线,∴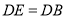 .∴
.∴ .
.
∵ ,
,
∴ .
.
∵ 是圆
是圆 的切线,
的切线, 是圆
是圆 的割线,
的割线,
∴ ,∴
,∴
考点:圆的基本性质.
【题型】解答题
【适用】一般
【标题】2016届广东省惠州市高三上学期第二次调研考试文科数学试卷(带解析)
【关键字标签】
【结束】
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系 中,直线
中,直线 的参数方程
的参数方程 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线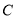 的极坐标方程为:
的极坐标方程为: .
.
(Ⅰ)求直线 的极坐标方程;
的极坐标方程;
(Ⅱ)求直线 与曲线
与曲线 交点的极坐标
交点的极坐标 .
.
科目:高中数学 来源:2016届四川省巴中市普通高中高三10月零诊考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-1:几何证明选讲
如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x方程x2-14x+mn=0的两个根.

(1)证明:C,B,D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北荆州中学高二上学期期中理科数学试卷(解析版) 题型:解答题
(本小题满分10分)某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:

分组 | 频数 |
[0,0.5) | 4 |
[0.5,1) | 8 |
[1,1.5) | 15 |
[1.5,2) | 22 |
[2,2.5) | 25 |
[2.5,3) | 14 |
[3,3.5) | 6 |
[3.5,4) | 4 |
[4,4.5] | 2 |
合计 | 100 |
(1)根据频率分布直方图估计这组数据的众数与平均数;
(2)当地政府制定了人均月用水量为3t的标准,若超出标准加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗?为什么?
查看答案和解析>>
科目:高中数学 来源:2014-2015学年海南省高三下学期大测三文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线C的极坐标方程是ρ=4cosθ,以极点为平面直角坐标系的原点,极轴为χ轴的正半轴,建立平
面直角坐标系,直线l的参数方程是 (t是参数).
(t是参数).
(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,直线l的参数方程化为普通方程;
(Ⅱ)若直线l与曲线C相交于A、B两点,且|AB|= ,试求实数m的值.
,试求实数m的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北武汉外国语学校高二上学期期中考试文科数学试卷(解析版) 题型:解答题
(本题12分)已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为 ,且过点(4,-
,且过点(4,- ).
).
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(3)在(2)的条件下求△F1MF2的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com