
【题目】设点(a,b)是区域 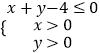 内的任意一点,则使函数f(x)=ax2﹣2bx+3在区间[
内的任意一点,则使函数f(x)=ax2﹣2bx+3在区间[ ![]() ,+∞)上是增函数的概率为( )
,+∞)上是增函数的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,
倍,![]() 为侧棱
为侧棱![]() 上的点.
上的点.
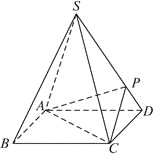
(1)求证:![]() .
.
(2)若![]() ⊥平面
⊥平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,若函数f(x)满足条件:存在[a,b]D,使f(x)在[a,b]上的值域是[2a,2b],则称f(x)为“倍扩函数”,若函数f(x)=log2(2x+t)为“倍扩函数”,则实数t的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接中国共产党的十九大的到来,某校举办了“祖国,你好”的诗歌朗诵比赛.该校高三年级准备从包括甲、乙、丙在内的7名学生中选派4名学生参加,要求甲、乙、丙这3名同学中至少有1人参加,且当这3名同学都参加时,甲和乙的朗诵顺序不能相邻,那么选派的4名学生不同的朗诵顺序的种数为( )
A. 720 B. 768 C. 810 D. 816
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(n)=1+ ![]() +
+ ![]() +…+
+…+ ![]() .经计算得f(4)>2,f(8)>
.经计算得f(4)>2,f(8)> ![]() ,f(16)>3,f(32)>
,f(16)>3,f(32)> ![]() .
.
(1)由上面数据,试猜想出一个一般性结论;
(2)用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC﹣A1B1C1中,AA1⊥底面A1B1C1 , 底面为直角三角形,∠ACB=90°,AC=2,BC=1,CC1= ![]() ,P是BC1上一动点,则A1P+PC的最小值是 .
,P是BC1上一动点,则A1P+PC的最小值是 . 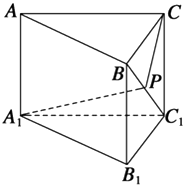
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:若实数x满足x2﹣4ax+3a2≤0,其中a>0;命题q:实数x满足 ![]()
(1)若a=1且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com