
分析 (1)根据数列的通项an和Sn的关系,即可求解数列{an}的通项公式;
(2)由bn=2+$\frac{1}{2}$($\frac{1}{n+1}$-$\frac{1}{n+3}$),即可利用裂项相消求解数列的和,得以证明.
解答 解:(1)当n≥2时,
an=Sn-Sn-1
=$\frac{{n}^{2}}{2}$+$\frac{3n}{2}$-$\frac{{(n-1)}^{2}}{2}$-$\frac{3(n-1)}{2}$
=n+1,
又n=1时,
a1=S1=2适合an=n+1,
∴an=n+1
(2)证明:由(1)知:
bn=n+3-(n+1)+$\frac{1}{(n+3)(n+1)}$
=2+$\frac{1}{2}$×($\frac{1}{n+1}$-$\frac{1}{n+3}$),
∴Tn=b1+b2+b3+…+bn
=2n+$\frac{1}{2}$×($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{n+1}$-$\frac{1}{n+3}$)
=2n+$\frac{1}{2}$×($\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{n+2}$-$\frac{1}{n+3}$)
<2n+$\frac{5}{12}$.
点评 本题考查了数列的通项公式an与前n项和Sn公式的应用问题,也考查了数列求和公式的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | f(sinA)<f(sinB) | B. | f(cosA)>f(cosB) | C. | f(sinA)<f(cosB) | D. | f(sinA)>f(cosB) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | [2,+∞) | C. | (2,+∞) | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
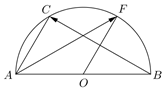 以AB为直径的半圆,|$\overrightarrow{AB}$|=2,O为圆心,C是$\widehat{AB}$上靠近点A的三等分点,F是$\widehat{AB}$上的某一点,若$\overrightarrow{AC}$∥$\overrightarrow{OF}$,则$\overrightarrow{AF}$•$\overrightarrow{BC}$=$-\frac{3}{2}$.
以AB为直径的半圆,|$\overrightarrow{AB}$|=2,O为圆心,C是$\widehat{AB}$上靠近点A的三等分点,F是$\widehat{AB}$上的某一点,若$\overrightarrow{AC}$∥$\overrightarrow{OF}$,则$\overrightarrow{AF}$•$\overrightarrow{BC}$=$-\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com