
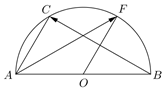
 以AB为直径的半圆,|$\overrightarrow{AB}$|=2,O为圆心,C是$\widehat{AB}$上靠近点A的三等分点,F是$\widehat{AB}$上的某一点,若$\overrightarrow{AC}$∥$\overrightarrow{OF}$,则$\overrightarrow{AF}$•$\overrightarrow{BC}$=$-\frac{3}{2}$.
以AB为直径的半圆,|$\overrightarrow{AB}$|=2,O为圆心,C是$\widehat{AB}$上靠近点A的三等分点,F是$\widehat{AB}$上的某一点,若$\overrightarrow{AC}$∥$\overrightarrow{OF}$,则$\overrightarrow{AF}$•$\overrightarrow{BC}$=$-\frac{3}{2}$. 分析 可以点O为坐标原点,AB所在直线为x轴建立平面直角坐标系,并连接OC,根据条件可得出∠COA=∠FOB=60°,并且OC=OF=1,这样即可求出点A,B,C,F的坐标,进而得出向量$\overrightarrow{AF},\overrightarrow{BC}$的坐标,从而得出$\overrightarrow{AF}•\overrightarrow{BC}$的值.
解答 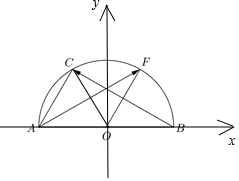 解:以O为原点,OB所在直线为x轴,
解:以O为原点,OB所在直线为x轴,
建立如图所示平面直角坐标系:
连接OC,据题意,∠COA=60°;
∴∠CAO=FOB=60°;
且OC=OF=1;
∴$A(-1,0),F(\frac{1}{2},\frac{\sqrt{3}}{2}),B(1,0),C(-\frac{1}{2},\frac{\sqrt{3}}{2})$;
∴$\overrightarrow{AF}=(\frac{3}{2},\frac{\sqrt{3}}{2}),\overrightarrow{BC}=(-\frac{3}{2},\frac{\sqrt{3}}{2})$;
∴$\overrightarrow{AF}•\overrightarrow{BC}=-\frac{9}{4}+\frac{3}{4}=-\frac{3}{2}$.
故答案为:$-\frac{3}{2}$.
点评 考查等弧所对的圆心角相等,通过建立平面直角坐标系,利用坐标解决向量问题的方法,以及根据点的坐标求向量坐标的方法,向量数量积的坐标运算.


科目:高中数学 来源: 题型:选择题
| A. | 关于直线x=1对称 | B. | 关于直线y=x对称 | ||
| C. | 关于直线y=-1对称 | D. | 关于直线y=1对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 底面半径为1,且体积为$\frac{4π}{3}$的圆锥 | B. | 底面积为1,高为$\sqrt{14}$的正四棱柱 | ||
| C. | 棱长为3的正四面体 | D. | 棱长为3的正方体 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com