
分析 (1)由已知利用换元法求得函数解析式;
(2)直接利用函数单调性的定义证明;
(3)由(2)结合函数的奇偶性把不等式f(t2-2t)+f(3t2-k)<0恒成立转化为t2-2t>k-3t2.分离k后求出函数4t2-2t的值域得答案.
解答 解:(1)∵f(log2x)=$\frac{-x+a}{x+1}$,∴令t=log2x,
则x=2t,代入原式中:f(t)=$\frac{-{2}^{t}+a}{{2}^{t}+a}$,则f(x)=$\frac{-{2}^{x}+a}{{2}^{x}+a}$,
又∵f(x)在R上是奇函数,∴f(0)=0,解得a=1.
则f(x)=$\frac{-{2}^{x}+a}{{2}^{x}+a}$;
(2)由(1)知$f(x)=\frac{{-{2^x}+1}}{{{2^x}+1}}=\frac{2}{{{2^x}+1}}-1$,
设x1<x2,则f(x1)-f(x2)=$\frac{2}{{{2^{x_1}}+1}}-\frac{2}{{{2^{x_2}}+1}}$=$\frac{{2({2^{x_2}}-{2^{x_1}})}}{{({{2^{x_1}}+1})({{2^{x_2}}+1})}}$.
∵函数y=2x在R上是增函数且x1<x2,
∴${2^{x_2}}$-${2^{x_1}}$>0.
又(${2^{x_1}}$+1)( ${2^{x_2}}$+1)>0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴f(x)在(-∞,+∞)上为减函数;
(3)∵f(x)是奇函数,
从而不等式:f(t2-2t)+f(3t2-k)<0等价于f(t2-2t)<-f(3t2-k)=f(k-3t2),
∵f(x)为减函数,由上式推得:t2-2t>k-3t2.
即对一切t∈[1,2]有:4t2-2t-k>0,k<4t2-2t,
当t=1时最小,则{k|k<2}.
点评 本题考查函数恒成立问题,考查了函数单调性的证明及其应用,体现了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:填空题
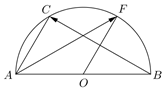 以AB为直径的半圆,|$\overrightarrow{AB}$|=2,O为圆心,C是$\widehat{AB}$上靠近点A的三等分点,F是$\widehat{AB}$上的某一点,若$\overrightarrow{AC}$∥$\overrightarrow{OF}$,则$\overrightarrow{AF}$•$\overrightarrow{BC}$=$-\frac{3}{2}$.
以AB为直径的半圆,|$\overrightarrow{AB}$|=2,O为圆心,C是$\widehat{AB}$上靠近点A的三等分点,F是$\widehat{AB}$上的某一点,若$\overrightarrow{AC}$∥$\overrightarrow{OF}$,则$\overrightarrow{AF}$•$\overrightarrow{BC}$=$-\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
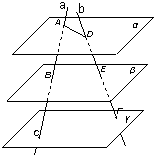 如图,平面α∥平面β∥平面γ,两条直线a,b分别与平面α,β,γ相交于点A,B,C和点D,E,F.已知AB=2cm,DE=4cm,EF=3cm,则AC的长为$\frac{7}{2}$cm.
如图,平面α∥平面β∥平面γ,两条直线a,b分别与平面α,β,γ相交于点A,B,C和点D,E,F.已知AB=2cm,DE=4cm,EF=3cm,则AC的长为$\frac{7}{2}$cm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com