
分析 (I)首先对f(x)求导,由已知f'(x)>0,x∈R,则△≤0,即可求出a的值;
(II)设切点为(x0,y0),则切线方程为:y=f'(x0)(x-x0)+y0,带入P点且只有一解,可求出a的值;
(III)切线方程为y=(${x}_{0}^{2}$-1)x-$\frac{2}{3}{x}_{0}^{3}$+1,令设g(x)=$\frac{2}{3}{x}^{3}$-mx2+m+n-1,可利用导数求出函数的极大值与极小值,直线有三条,则则g(0)>0,g(m)<0.
解答 解:(I)f'(x)=x2+ax+a-1;
由已知f'(x)>0,x∈R;
∴△≤0,有△=a2-4(a-1)=(a-2)2;
∴a=2;
故a的取值集合为{2}.
(II)设切点为(x0,y0),则切线方程为:
y=f'(x0)(x-x0)+y0;
y=(${x}_{0}^{2}$+ax0+a-1)x-$\frac{2}{3}{x}_{0}^{3}$-$\frac{a}{2}{x}_{0}^{2}$+1;
∵切线过点P(0,1)
∴$\frac{2}{3}{x}_{0}^{3}$+$\frac{a}{2}{x}_{0}^{2}$=0 ①;
由已知,①只有一解,故a=0.
(III)由(II)知,切线方程为y=(${x}_{0}^{2}$-1)x-$\frac{2}{3}{x}_{0}^{3}$+1;
切线过点Q(m,n);
∴$\frac{2}{3}{x}_{0}^{3}-m{x}_{0}^{2}+m+n-1$=0;
设g(x)=$\frac{2}{3}{x}^{3}$-mx2+m+n-1;
g'(x)=2x(x-m);
y=g(x)的极大值为g(0)=m+n-1;
y=g(x)的极小值为:g(m)=-$\frac{1}{3}{m}^{3}$+m+n-1;
切线有3条,则g(0)>0,g(m)<0;
即:-m+1<n<$\frac{1}{3}{m}^{3}$-m+1.
故得证.
点评 本题主要考查了利用二次函数的图形特征,切线方程以及利用导数判断函数的单调性,属中等题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的$\frac{1}{4}$.
高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
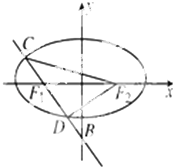 已知椭圆$\frac{x^2}{2}+{y^2}=1$及点B(0,-3),过左焦点F1与B的直线交椭圆于C,D两点,F2为椭圆的右焦点,求△CDF2的面积.
已知椭圆$\frac{x^2}{2}+{y^2}=1$及点B(0,-3),过左焦点F1与B的直线交椭圆于C,D两点,F2为椭圆的右焦点,求△CDF2的面积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
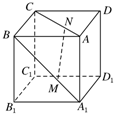 如图所示,正方体ABCD-A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=$\frac{\sqrt{2}a}{3}$,则MN与平面BB1C1C的位置关系是( )
如图所示,正方体ABCD-A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=$\frac{\sqrt{2}a}{3}$,则MN与平面BB1C1C的位置关系是( )| A. | 相交 | B. | 平行 | C. | 垂直 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com