
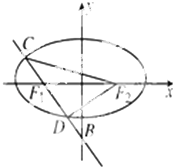
 已知椭圆$\frac{x^2}{2}+{y^2}=1$及点B(0,-3),过左焦点F1与B的直线交椭圆于C,D两点,F2为椭圆的右焦点,求△CDF2的面积.
已知椭圆$\frac{x^2}{2}+{y^2}=1$及点B(0,-3),过左焦点F1与B的直线交椭圆于C,D两点,F2为椭圆的右焦点,求△CDF2的面积. 分析 解法一:椭圆$\frac{{x}^{2}}{2}$+y2=1左焦点是F1,直线CD方程为y=-3x-3,与椭圆方程联立化为:19x2+36x+16=0,而△>0,设C(x1,y1),D(x2,y2),利用搞一下试试的关系可得:|CD|=$\sqrt{(1+{3}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$,又F2到直线DC的距离d,可得△CDF2的面积S=$\frac{1}{2}$|CD|•d.
解法二:直线CD方程为y=-3x-3,与椭圆方程联立去x得:19y2+6y-9=0,可得|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$,利用△CDF2的面积S=$\frac{1}{2}$|F1F2|•|y1-y2|,即可得出.
解答 解:解法一:∵椭圆$\frac{{x}^{2}}{2}$+y2=1左焦点是F1,∴F1(-1,0),∴直线CD方程为y=-3x-3,
由$\left\{\begin{array}{l}y=-3x-3\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$,得19x2+36x+16=0,而△>0,
设C(x1,y1),D(x2,y2),则$\left\{\begin{array}{l}{x_1}+{x_2}=-\frac{36}{19}\\{x_1}{x_2}=\frac{16}{19}\end{array}\right.$,
∴$|CD|=\sqrt{{{({x_1}-{x_2})}^2}+{{({y_1}-{y_2})}^2}}=\sqrt{(1+9)[{{(-\frac{36}{19})}^2}-4×\frac{64}{19}]}=\frac{{20\sqrt{2}}}{9}$.
又F2到直线DC的距离$d=\frac{6}{{\sqrt{10}}}$,
故△CDF2的面积S=$\frac{1}{2}$|CD|•d=$\frac{{12\sqrt{5}}}{19}$.
解法二∵椭圆$\frac{{x}^{2}}{2}$+y2=1左焦点是F1(-1,0),
∴直线CD方程为y=-3x-3,
联立$\left\{\begin{array}{l}y=-3x-3\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$消去x得:19y2+6y-9=0,而△>0,
∴$\left\{\begin{array}{l}{y_1}+{y_2}=-\frac{6}{19}\\{y_1}{y_2}=-\frac{9}{19}\end{array}\right.$,
∴$|{y_1}-{y_2}|=\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}=\sqrt{{{(-\frac{6}{19})}^2}+\frac{36}{19}}=\frac{{12\sqrt{5}}}{19}$,
又|F1F2|=2,
∴△CDF2的面积S=$\frac{1}{2}$|F1F2|•|y1-y2|=$\frac{{12\sqrt{5}}}{19}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长公式、三角形面积计算公式、点到直线的距离公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (15,3) | B. | (16,2) | C. | (14,4) | D. | (17,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 嗜酒 | 不嗜酒 | 总计 | |
| 患肝病 | 20 | 10 | 30 |
| 不患肝病 | 30 | 45 | 75 |
| 总计 | 50 | 55 | 105 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 10% | B. | 5% | C. | 2.5% | D. | 1% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com