
分析 对已知等式变心求得tanC的值进而求得C,然后利用正弦的两角和公式求得cosAsinB的值,最后利用正弦的两角和公式求得sin(A-B)=0,判断出A=B,最后推断出三角形为正三角形.
解答 解:△ABC中,∵tanA+tanB+$\sqrt{3}$=$\sqrt{3}$tanAtanB,sinAcosB=$\frac{\sqrt{3}}{4}$,
∴tan(A+B)=$\frac{tanA+tanB}{1-tanAtanB}$=$\frac{\sqrt{3}•(tanAtanB-1)}{1-tanAtanB}$=-$\sqrt{3}$=-tanC,∴tanC=$\sqrt{3}$,∴C=$\frac{π}{3}$,A+B=$\frac{2π}{3}$.
又sinAcosB=$\frac{\sqrt{3}}{4}$,sinC=sin(A+B)=sinAcosB+cosAsinB=$\frac{\sqrt{3}}{2}$,
∴cosAsinB=$\frac{\sqrt{3}}{4}$,∴sin(A-B)=sinAcosB-cosAsinB=0,∴A=B,∴△ABC为等边三角形,
故答案为:等边三角形.
点评 本题主要考查了两角和与差的正弦函数和正弦函数公式的应用.考查了学生对三角函数公式的灵活运用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,$\frac{3}{2}$] | B. | [0,$\frac{9}{2}$] | C. | [-3,15] | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
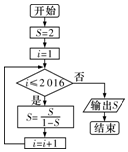
| A. | -$\frac{2}{4029}$ | B. | -$\frac{2}{4030}$ | C. | -$\frac{2}{4031}$ | D. | -$\frac{2}{4033}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [2,3] | C. | [1,2]或[2,3]都可以 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
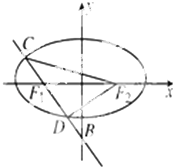 已知椭圆$\frac{x^2}{2}+{y^2}=1$及点B(0,-3),过左焦点F1与B的直线交椭圆于C,D两点,F2为椭圆的右焦点,求△CDF2的面积.
已知椭圆$\frac{x^2}{2}+{y^2}=1$及点B(0,-3),过左焦点F1与B的直线交椭圆于C,D两点,F2为椭圆的右焦点,求△CDF2的面积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com