
分析 (1)函数f(x)=x2+bx+c,f(-3)=f(1),f(0)=-3,带入求b,c的值可得f(x)的解析式;
(2)求出g(x)的表达式,在画图象.
(3)数形结合法,根据图象求[-3,1]的最大值和最小值.
解答 解:(1)由题意:函数f(x)=x2+bx+c满足f(-3)=f(1),f(0)=-3.
则有:$\left\{\begin{array}{l}{1+b+c=9x-3b+c}\\{c=-3}\end{array}\right.$
解得:b=2,c=-3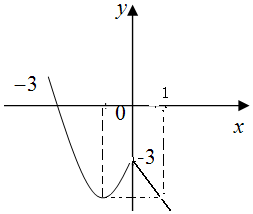
∴函数f(x)的解析式为f(x)=x2+2x-3.
(2)由(1)可知b=2,c=-3,
函数g(x)=$\left\{\begin{array}{l}{{x}^{2}+bx+c,x≤0}\\{-3-x,x>0}\end{array}\right.$
⇒g(x)=$\left\{\begin{array}{l}{{x}^{2}+2x-3,(x≤0)}\\{-3-x,(x>0)}\end{array}\right.$.
图象如右图所示:
(3)由(2)中的图象可知:(-3,-1)是单调减区间,(-1,0)是单调增区间
(0,1)是单调减区间
则:g(1)=-4,g(-1)=-4,g(-3)=0
∴函数g(x)在[-3,1]的最大值为0,最小值为-4.
点评 本题考查了分段函数的解析式的求法和图象的画法,通过数形结合求解定义域范围内的值域问题.属于中档题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
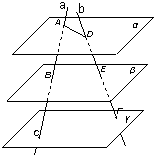 如图,平面α∥平面β∥平面γ,两条直线a,b分别与平面α,β,γ相交于点A,B,C和点D,E,F.已知AB=2cm,DE=4cm,EF=3cm,则AC的长为$\frac{7}{2}$cm.
如图,平面α∥平面β∥平面γ,两条直线a,b分别与平面α,β,γ相交于点A,B,C和点D,E,F.已知AB=2cm,DE=4cm,EF=3cm,则AC的长为$\frac{7}{2}$cm.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (15,3) | B. | (16,2) | C. | (14,4) | D. | (17,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 嗜酒 | 不嗜酒 | 总计 | |
| 患肝病 | 20 | 10 | 30 |
| 不患肝病 | 30 | 45 | 75 |
| 总计 | 50 | 55 | 105 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 10% | B. | 5% | C. | 2.5% | D. | 1% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com