
分析 (1)令x=a,则f(a)=2,从而可知f(x)过定点(a,2),再由题设即可求得a值;
(2)根据图象平移规则:左加右减,上加下减即可求得g(x)表达式,从而可得h(x)的解析式;
(3)令t=log3x,则t∈[0,2],不等式[h(x)+2]2≤h(x2)+m+6 恒成立,可转化为关于t的二次不等式恒成立,进而转化为求函数的最值解决,利用二次函数的性质易求其最值;
解答 解:(1)由已知a2-a+1=2,∴a=2.
(2)∵f(x)=2x-2+1,
∴g(x)=2x,
∴h(x)=log2x(x>0),
(3)要使不等式有意义:则有1<x≤4且1<x2≤4,
∴1<x≤2,
据题有${({log_2}x+2)^2}≤{log_2}{x^2}+m{log_2}x+6$在(1,2]恒成立,
∴设t=log2x(1<x≤2),
∴0<t≤1,
∴(t+2)2≤2t+tm+6在(0,1]时恒成立.
即:$m≥\frac{{{t^2}+2t-2}}{t}=t-\frac{2}{t}+2$在[0,1]时恒成立,
设$y=t-\frac{2}{t}+2$,t∈(0,1]单调递增,
∴t=1时,有ymax=1,
∴m≥1.
点评 本题考查函数恒成立问题,考查函数图象变换及反函数,考查学生分析问题解决问题的能力,解决恒成立问题的基本思路是转化为函数的最值解决.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,$\frac{3}{2}$] | B. | [0,$\frac{9}{2}$] | C. | [-3,15] | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,1) | B. | (-5,1) | C. | ($\frac{1}{2}$,1) | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
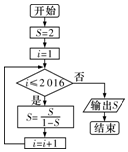
| A. | -$\frac{2}{4029}$ | B. | -$\frac{2}{4030}$ | C. | -$\frac{2}{4031}$ | D. | -$\frac{2}{4033}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
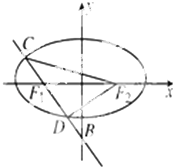 已知椭圆$\frac{x^2}{2}+{y^2}=1$及点B(0,-3),过左焦点F1与B的直线交椭圆于C,D两点,F2为椭圆的右焦点,求△CDF2的面积.
已知椭圆$\frac{x^2}{2}+{y^2}=1$及点B(0,-3),过左焦点F1与B的直线交椭圆于C,D两点,F2为椭圆的右焦点,求△CDF2的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com