练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．若平面内有n（n≥4）个点，满足任意三点都不共线，且任意两点构成的向量与其余任意两点构成的向量的数量积为0，则n的最大值为（　　）
    A．3B．4C．5D．不存在

    分析 根据题意画出图形，然后根据条件所给任意三点要构成直角三角形进行判断假设即可．

    解答 解：任意两点构成的向量与其余任意两点构成的向量的数量积为0，
    则任意三点所构成的三角形为直角三角形，
    如下图所示：
    三个点ABC构成直角三角形，现在加一点D并使其满足题意，
    ①若ABD中斜边不是AB（如图一）则∠CBD为钝角，三角形CBD不为直角三角形，矛盾；
    ②故AB为三角形ABD斜边，即D在AB为直径的圆上，又ACD，BCD是直角三角形，所以只能CD是直径，
    即n=4时满足．
    ③若存在异于D的第5点E满足题意，由①知E比在ABC确定的圆上，则CE不为直径，
    ∠CAE与∠CBE中必有一个角为钝角，矛盾．
    综上n最大为4．
    故选：B．

    点评 本题考查学生的思维和动手能力，关键是读懂题意，所给三点必须要构成直角三角形，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

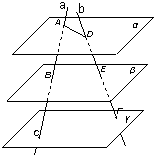    2．如图，平面α∥平面β∥平面γ，两条直线a，b分别与平面α，β，γ相交于点A，B，C和点D，E，F．已知AB=2cm，DE=4cm，EF=3cm，则AC的长为$\frac{7}{2}$cm．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知f（x）=$\frac{1}{3}{x^3}+\frac{a}{2}{x^2}+（{a-1}）x+1$，x∈R，其中参数a∈R．
    （Ⅰ）是否存在a，使得f（x）在R上单调递增，若存在求a的取值集合，不存在说明理由；
    （Ⅱ）若过点P（0，1）且与y=f（x）相切的直线有且只有一条，求a的值；
    （Ⅲ）在（Ⅱ）的条件下，设点Q（m，n），且m＞0，证明：若过Q且与曲线y=f（x）相切的直线有三条，则-m+1＜n＜$\frac{1}{3}{m^3}$-m+1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知a＞0，b＞0且a≠b，设x=$\frac{{\sqrt{a}+\sqrt{b}}}{2}$，$y=\sqrt{a+b}$，$z=\root{4}{ab}$，则x，y，z的大小关系是（　　）
    A．y＞x＞zB．x＞y＞zC．y＞z＞xD．z＞y＞x

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．根据下列2×2列联表，判断“患肝病和嗜酒有关系”犯错误的概率不会超过（　　）
    嗜酒不嗜酒总计
    患肝病201030
    不患肝病304575
    总计5055105
    卡方临界值表
    P（K2≥k0）0.500.400.250.150.100.050.0250.0100.0050.001
    k00.4550.7081.3232.0722.7063.8415.0246.6357.87910.828
    A．10%B．5%C．2.5%D．1%

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．全集U={1，2，3，4，5}，若A={1，2}，B={1，4}，则∁U（A∪B）={3，5}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知幂函数$f（x）={x^{{m^2}-2m-3}}（m∈Z）$为偶函数，且在（0，+∞）上是减函数，则f（x）的解析式是f（x）=x-4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知向量$\overrightarrow a=（1，\sqrt{3}），\overrightarrow b=（0，1）$，则$\overrightarrow a$在$\overrightarrow b$方向上的投影是$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．先后抛掷质地均匀的硬币两次，则“一次正面向上，一次反面向上”的概率为（　　）
    A．$\frac{1}{4}$B．$\frac{1}{2}$C．$\frac{2}{3}$D．$\frac{3}{4}$

    查看答案和解析>>

    同步练习册答案