
分析 由幂函数f(x)为(0,+∞)上递减,推知m2-2m-3<0,解得-1<m<3因为m为整数故m=0,1或2,又通过函数为偶函数,推知m2-2m-3为偶数,进而推知m2-2m为奇数,进而推知m只能是1,把m代入函数,即可得到f(x)的解析式.
解答 解:∵幂函数f(x)=xm2-2m-3(m∈Z)为偶函数,且在区间(0,+∞)上是减函数,
∴m2-2m-3<0,解得-1<m<3,
∵m为整数,∴m=0,1或2,
又∵函数为偶函数,∴m2-2m-3为偶数,
∴m2-2m为奇数,∴m只能是1,
把m=1代入函数f(x)=xm2-2m-3,
得f(x)=x-4.
故答案为f(x)=x-4.
点评 本题考查函数的解析式的求法,幂函数的性质的合理运用是关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
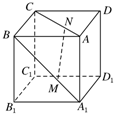 如图所示,正方体ABCD-A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=$\frac{\sqrt{2}a}{3}$,则MN与平面BB1C1C的位置关系是( )
如图所示,正方体ABCD-A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=$\frac{\sqrt{2}a}{3}$,则MN与平面BB1C1C的位置关系是( )| A. | 相交 | B. | 平行 | C. | 垂直 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$] | B. | (0,1) | C. | [$\frac{1}{2}$,3) | D. | (0,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com