Question

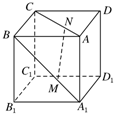
13．如图所示，正方体ABCD-A₁B₁C₁D₁的棱长为a，M，N分别为A₁B和AC上的点，A₁M=AN=$\frac{\sqrt{2}a}{3}$，则MN与平面BB₁C₁C的位置关系是（　　）

• A． 相交
• B． 平行
• C． 垂直
• D． 不能确定

Answer 1

分析 由于CD⊥平面B₁BCC₁，所以$\overrightarrow{CD}$是平面B₁BCC₁的法向量，因此只需证明向量$\overrightarrow{MN}$与$\overrightarrow{CD}$垂直即可，而$\overrightarrow{CD}$与$\overrightarrow{{B}_{1}B}$和$\overrightarrow{{B}_{1}{C}_{1}}$均垂直，而$\overrightarrow{{B}_{1}B}$和$\overrightarrow{{B}_{1}{C}_{1}}$又可以作为一组基底表示向量$\overrightarrow{MN}$，因此可以证明．

解答 解：∵正方体棱长为a，A₁M=AN=$\frac{\sqrt{2}a}{3}$，
∴$\overrightarrow{MB}$=$\frac{2}{3}$$\overrightarrow{{A}_{1}B}$，$\overrightarrow{CN}$=$\frac{2}{3}$$\overrightarrow{CA}$，
∴$\overrightarrow{MN}$=$\overrightarrow{MB}$+$\overrightarrow{BC}$+$\overrightarrow{CN}$=$\frac{2}{3}$$\overrightarrow{{A}_{1}B}$+$\overrightarrow{BC}$+$\frac{2}{3}$$\overrightarrow{CA}$=$\frac{2}{3}$（$\overrightarrow{{A}_{1}{B}_{1}}$+$\overrightarrow{{B}_{1}B}$）+$\overrightarrow{BC}$+$\frac{2}{3}$（$\overrightarrow{CD}$+$\overrightarrow{DA}$）
=$\frac{2}{3}$$\overrightarrow{{B}_{1}B}$+$\frac{1}{3}$$\overrightarrow{{B}_{1}{C}_{1}}$．
又∵$\overrightarrow{CD}$是平面B₁BCC₁的法向量，
且$\overrightarrow{MN}$•$\overrightarrow{CD}$=（$\frac{2}{3}$$\overrightarrow{{B}_{1}B}$+$\frac{1}{3}$$\overrightarrow{{B}_{1}{C}_{1}}$）•$\overrightarrow{CD}$=0，
∴$\overrightarrow{MN}$⊥$\overrightarrow{CD}$，
∴MN∥平面B₁BCC₁．
故选：B．

点评 本题考查线面平行的判定，在适当条件下，可以用向量法证明，只需证明该直线的一个方向向量与该平面的一个法向量垂直即可．要注意的是这两个向量必须用同一组基底来表示．