
| A. | f(sinA)<f(sinB) | B. | f(cosA)>f(cosB) | C. | f(sinA)<f(cosB) | D. | f(sinA)>f(cosB) |
分析 先求导,求出函数的单调减区间,再根据诱导公式和三角形的内角的关系得到答案.
解答 解:f′(x)=3x2-3,
令f′(x)=0,解得x=±1,
当f′(x)≤0时,即-1≤x≤1时,函数单调递减,
∵△ABC中,C为钝角,
∴90°<C<180°,
∴0<B+A<90°,
∴0<B<90°-A<90°,
∴sinB<sin(90°-A)=cosA,cosB>cos(90°-A)=sinA,
∴f(sinB)>f(cosA),f(cosB)>f(sinA),
∵A,B的大小无法判断,
∴sinA与sinB,cosA与cosB无法判断,
故选:C
点评 本题考查了导数和函数的单调性的关系和三角形中的角的关系和三角函数的值域以及单调性,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | △PF1F2的内切圆的圆心必在直线x=a上 | |
| B. | △PF1F2的内切圆的圆心必在直线x=b上 | |
| C. | △PF1F2的内切圆的圆心必在直线OP上 | |
| D. | △PF1F2的内切圆必通过点(b,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
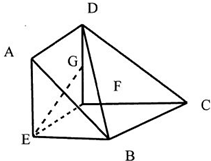 已知直角梯形ABCD中,AD⊥AB,AB∥DC,AB=2,DC=3,E为AB的中点,过E作EF∥AD,将四边形AEFD沿EF折起使面AEFD⊥面EBCF.
已知直角梯形ABCD中,AD⊥AB,AB∥DC,AB=2,DC=3,E为AB的中点,过E作EF∥AD,将四边形AEFD沿EF折起使面AEFD⊥面EBCF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | [2,+∞) | C. | [2,$\frac{7}{2}$] | D. | [$\frac{7}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于直线x=1对称 | B. | 关于直线y=x对称 | ||
| C. | 关于直线y=-1对称 | D. | 关于直线y=1对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com