
如图,
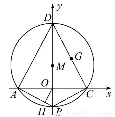
在平面直角坐标系中,方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上.
(1)求证:F<0.
(2)若四边形ABCD的面积为8,对角线AC的长为2,且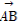 ·
·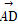 =0,求D2+E2-4F的值.
=0,求D2+E2-4F的值.
(3)设四边形ABCD的一条边CD的中点为G,OH⊥AB且垂足为H.试用平面解析几何的研究方法判断点O,G,H是否共线,并说明理由.
(1)见解析 (2)64 (3) O,G,H三点必定共线,理由见解析
【解析】(1)方法一:由题意,原点O必定在圆M内,即点(0,0)代入方程x2+y2+Dx+Ey+F=0的左边所得的值小于0,于是有F<0,即证.
方法二:由题意,不难发现A,C两点分别在x轴正、负半轴上.设两点坐标分别为A(a,0),C(c,0),则有ac<0.对于圆的方程x2+y2+Dx+Ey+F=0,当y=0时,可得x2+Dx+F=0,其中方程的两根分别为点A和点C的横坐标,于是有xAxC=ac=F.
因为ac<0,故F<0.
(2)不难发现,对角线互相垂直的四边形ABCD的面积S=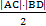 ,因为S=8,|AC|=2,可得|BD|=8.
,因为S=8,|AC|=2,可得|BD|=8.
又因为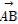 ·
·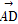 =0,所以∠BAD为直角,又因为四边形是圆M的内接四边形,故|BD|=2r=8⇒r=4.
=0,所以∠BAD为直角,又因为四边形是圆M的内接四边形,故|BD|=2r=8⇒r=4.
对于方程x2+y2+Dx+Ey+F=0所表示的圆,
可知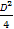 +
+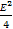 -F=r2,所以D2+E2-4F=4r2=64.
-F=r2,所以D2+E2-4F=4r2=64.
(3)设四边形四个顶点的坐标分别为A(a,0),B(0,b),C(c,0),D(0,d).
则可得点G的坐标为(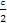 ,
,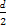 ),即
),即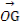 =(
=(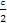 ,
,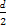 ).
).
又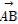 =(-a,b),且AB⊥OH,故要使G,O,H三点共线,只需证
=(-a,b),且AB⊥OH,故要使G,O,H三点共线,只需证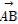 ·
·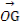 =0即可.
=0即可.
而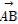 ·
·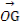 =
=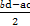 ,且对于圆M的一般方程x2+y2+Dx+Ey+F=0,
,且对于圆M的一般方程x2+y2+Dx+Ey+F=0,
当y=0时可得x2+Dx+F=0,其中方程的两根分别为点A和点C的横坐标,
于是有xAxC=ac=F.
同理,当x=0时,可得y2+Ey+F=0,其中方程的两根分别为点B和点D的纵坐标,于是有yByD=bd=F.
所以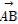 ·
·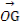 =
=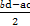 =0,即AB⊥OG.
=0,即AB⊥OG.
故O,G,H三点必定共线.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业八十一选修4-5第三节练习卷(解析版) 题型:解答题
已知实数a,b,c满足a+b+c=2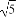 ,求a2+2b2+c2的最小值.
,求a2+2b2+c2的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十六第八章第七节练习卷(解析版) 题型:选择题
设抛物线y2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是( )
(A)4 (B)6 (C)8 (D)12
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十五第八章第六节练习卷(解析版) 题型:解答题
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为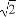 ,且过点P(4,-
,且过点P(4,-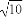 ).
).
(1)求双曲线的方程.
(2)若点M(3,m)在双曲线上,求证: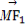 ·
·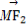 =0.
=0.
(3)求△F1MF2的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十五第八章第六节练习卷(解析版) 题型:选择题
双曲线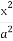 -
-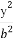 =1(a>0,b>0)的离心率为2,则
=1(a>0,b>0)的离心率为2,则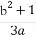 的最小值为( )
的最小值为( )
(A)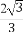 (B)
(B)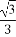 (C)2 (D)1
(C)2 (D)1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:填空题
圆C:x2+y2+2x-2y-2=0的圆心到直线3x+4y+14=0的距离是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:选择题
若曲线C:x2+y2+2ax-4ay+5a2-4=0上所有的点均在第二象限内,则a的取值范围为( )
(A)(-∞,-2) (B)(-∞,-1)
(C)(1,+∞) (D)(2,+∞)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十三第八章第四节练习卷(解析版) 题型:解答题
已知☉O:x2+y2=1和定点A(2,1),由☉O外一点P(a,b)向☉O引切线PQ,切点为Q,且满足|PQ|=|PA|.
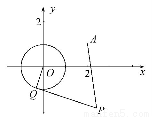
(1)求实数a,b间满足的等量关系.
(2)求线段PQ长的最小值.
(3)若以P为圆心所作的☉P与☉O有公共点,试求半径取最小值时☉P的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:选择题
点A(1,1)到直线xcosθ+ysinθ-2=0的距离的最大值是( )
(A)2 (B)2-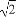
(C)2+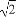 (D)4
(D)4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com