
分析 (1)由于(x2-1)+(x2+3x+2)i是纯虚数(i为虚数单位),可得$\left\{\begin{array}{l}{{x}^{2}-1=0}\\{{x}^{2}+3x+2≠0}\end{array}\right.$,解得x.
(2)设z=a+bi(a,b∈R),则$\overline{z}$=a-bi.根据${({z+\overline z})^2}$$-3z\overline z•i=4-12i$(i为虚数单位),可得4a2-3(a2+b2)i=4-12i.利用复数相等即可得出.
解答 解:(1)∵(x2-1)+(x2+3x+2)i是纯虚数(i为虚数单位),∴$\left\{\begin{array}{l}{{x}^{2}-1=0}\\{{x}^{2}+3x+2≠0}\end{array}\right.$,解得x=1.
(2)设z=a+bi(a,b∈R),则$\overline{z}$=a-bi.
∵${({z+\overline z})^2}$$-3z\overline z•i=4-12i$(i为虚数单位),
∴4a2-3(a2+b2)i=4-12i.
∴4a2=4,-3(a2+b2)=-12.
解得a=±1,b=$±\sqrt{3}$.
∴z=±1$±\sqrt{3}$i.
点评 本题考查了纯虚数的定义、共轭复数的定义、复数相等,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{{\sqrt{x}}}{2}$ | B. | y=(x-1)2 | C. | y=2-x | D. | y=log0.5x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为${P_0}(\frac{{\sqrt{3}}}{2},\frac{1}{2})$,秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )
为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为${P_0}(\frac{{\sqrt{3}}}{2},\frac{1}{2})$,秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )| A. | $y=sin(\frac{π}{30}t+\frac{π}{6})$ | B. | $y=sin(-\frac{π}{60}t-\frac{π}{6})$ | C. | $y=sin(-\frac{π}{30}t+\frac{π}{6})$ | D. | $y=sin(-\frac{π}{30}t-\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
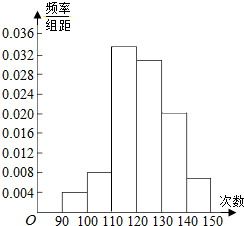 为了了解高一学生的体能情况,某校抽取部分学生进行一部分跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12,若次数在110以上(含110次)为达标,试估计该学校全体高一学生单调达标率是0.88.
为了了解高一学生的体能情况,某校抽取部分学生进行一部分跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12,若次数在110以上(含110次)为达标,试估计该学校全体高一学生单调达标率是0.88.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (1,2) | C. | (3,0) | D. | (0,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com