
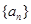 的首项
的首项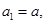 其中
其中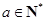 ,
,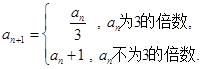 令集合
令集合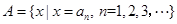 .
.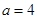 ,写出集合
,写出集合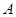 中的所有的元素;
中的所有的元素;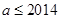 ,且数列
,且数列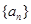 中恰好存在连续的7项构成等比数列,求
中恰好存在连续的7项构成等比数列,求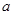 的所有可能取值构成的集合;
的所有可能取值构成的集合;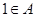 .
.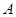 的所有元素为:4,5,6,2,3,1.
的所有元素为:4,5,6,2,3,1.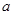 的所有可能取值的集合为{
的所有可能取值的集合为{ ,
,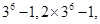
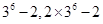 }.
}. 
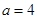 代入,依次写出集合
代入,依次写出集合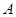 的所有元素.
的所有元素. ,关键是理解好“如果
,关键是理解好“如果 是3的倍数,则
是3的倍数,则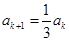 ;如果
;如果 是被3除余1,则由递推关系可得
是被3除余1,则由递推关系可得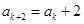 ,所以
,所以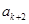 是3的倍数,所以
是3的倍数,所以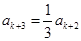 ;如果
;如果 被3除余2,则由递推关系可得
被3除余2,则由递推关系可得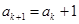 ,所以
,所以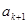 是3的倍数,所以
是3的倍数,所以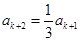 .”得到结论:该7项的等比数列的公比为
.”得到结论:该7项的等比数列的公比为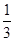 .
. 被3除余1,
被3除余1, 被3除余2,,
被3除余2,, 被3除余0”加以讨论,确定得到
被3除余0”加以讨论,确定得到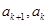 的关系为:
的关系为: ,
,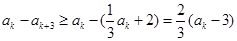
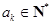 ,所以
,所以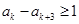 .数列
.数列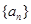 中必存在某一项
中必存在某一项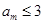 (否则会与上述结论矛盾!)
(否则会与上述结论矛盾!) ,
,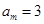 ,加以讨论,得到
,加以讨论,得到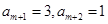 ,
,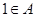 .
. 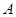 的所有元素为:4,5,6,2,3,1.. 3分
的所有元素为:4,5,6,2,3,1.. 3分 ,
, 是3的倍数,则
是3的倍数,则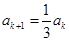 ;如果
;如果 是被3除余1,则由递推关系可得
是被3除余1,则由递推关系可得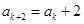 ,所以
,所以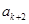 是3的倍数,所以
是3的倍数,所以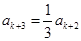 ;如果
;如果 被3除余2,则由递推关系可得
被3除余2,则由递推关系可得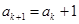 ,所以
,所以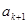 是3的倍数,所以
是3的倍数,所以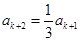 .
.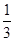 .
.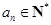 ,所以这7项中前6项一定都是3的倍数,而第7项一定不是3的倍数(否则构成等比数列的连续项数会多于7项),
,所以这7项中前6项一定都是3的倍数,而第7项一定不是3的倍数(否则构成等比数列的连续项数会多于7项),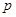 ,则
,则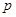 是被3除余1或余2的正整数,则可推得
是被3除余1或余2的正整数,则可推得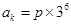
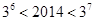 ,所以
,所以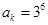 或
或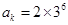 .
.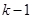 项中,满足小于2014的各项只有:
项中,满足小于2014的各项只有:
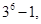 或
或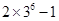 ,
,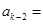
 或
或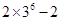 ,
,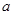 的所有可能取值的集合为
的所有可能取值的集合为 ,
,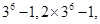
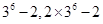 }. 8分
}. 8分 被3除余1,则由已知可得
被3除余1,则由已知可得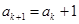 ,
,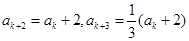 ;
; 被3除余2,则由已知可得
被3除余2,则由已知可得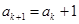 ,
,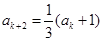 ,
,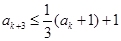 ;
; 被3除余0,则由已知可得
被3除余0,则由已知可得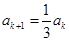 ,
, ;
; ,
,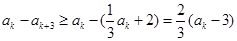
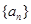 中的任意一项
中的任意一项 ,“若
,“若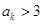 ,则
,则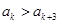 ”.
”.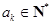 ,所以
,所以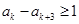 .
.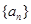 中必存在某一项
中必存在某一项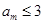 (否则会与上述结论矛盾!)
(否则会与上述结论矛盾!) ,结论得证.
,结论得证.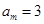 ,则
,则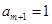 ;若
;若 ,则
,则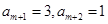 ,
,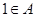 . 13分
. 13分

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com