
分析 (1)根据第三行成等差数列得出a3n,根据最后一列成等差数列得出a3n,从而得出d1,d2,d3的关系,同理根据amn的不同算法即可得出dm关于m,d1,d2的式子;
(2)根据分组特点计算cm,利用错位相减法计算Sn;
(3)把Sn,dn代入不等式求出使不等式成立的n的最小值即可得出N的最小值.
解答 解:(1)∵每一行都是首项为1的等差数列,
∴a1n=1+(n-1)d1,a2n=1+(n-1)d2,a3n=1+(n-1)d3.
∵每一列也是等差数列,∴2a2n=a1n+a3n,
∴2+2(n-1)d2=1+(n-1)d1+1+(n-1)d3,即2d2=d1+d3
∴d1,d2,d3成等差数列.
∵amn=1+(n-1)dm,
amn=a1n+(m-1)(a2n-a1n)=a1n+(m-1)(a2n-a1n)=1+(n-1)d1+(m-1)(n-1)(d2-d1),
∴1+(n-1)dm=1+(n-1)d1+(m-1)(n-1)(d2-d1)
化简得dm=(2-m)d1+(m-1)d2.
(2)当d1=1,d2=3时,dm=2m-1(m∈N*),
按数列{dm}分组规律,第m组中有2m-1个数,
所以第1组到第m组共有1+3+5+…+(2m-1)=m2个数.
则前m组的所有数字和为$\frac{{1+(2{m^2}-1)}}{2}•{m^2}={m^4}$,
∴${({c_m})^4}={m^4}$,∵cm>0,∴cm=m,
从而 ${2^{c_m}}{d_m}=(2m-1)•{2^m}$,m∈N*,
∴Sn=1×2+3×22+5×23+…+(2n-1)×2n,
∴2Sn=1×22+3×23+…+(2n-1)×2n+1,
∴-Sn=2+23+24+…+2n+1-(2n-1)×2n+1=2+23(2n-1-1)-(2n-1)×2n+1=(3-2n)×2n+1-6.
∴${S_n}=(2n-3)•{2^{n+1}}+6$.
(3)由$\frac{1}{50}({S_n}-6)>{d_n}$得(2n-3)•2n+1>50(2n-1).
令an=(2n-3)•2n+1-50(2n-1)=(2n-3)(2n+1-50)-100.
∴当n≤5时,an<0,当n≥6时,an>0,
所以,满足条件的所有正整数N=5,6,7,8,…,20.
点评 本题考查了等差数列的性质,数列求和,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | i | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
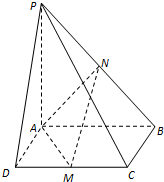 如图:已知四棱锥P-ABCD,底面是边长为6的正方形,PA=8,PA⊥面ABCD,
如图:已知四棱锥P-ABCD,底面是边长为6的正方形,PA=8,PA⊥面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| P(x2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com