
分析 由题意可得$\frac{1}{{{a}_{n+1}}^{2}}$-$\frac{1}{{{a}_{n}}^{2}}$=4,运用等差数列的通项公式可得$\frac{1}{{{a}_{n}}^{2}}$=4n-3,求得bn=$\frac{1}{4}$($\sqrt{4n+1}$-$\sqrt{4n-3}$),运用数列的求和方法:裂项相消求和,即可得到所求和.
解答 解:a1=1,$(\frac{1}{{{a_{n+1}}}}+\frac{1}{a_n})(\frac{1}{{{a_{n+1}}}}-\frac{1}{a_n})=4$,
可得$\frac{1}{{{a}_{n+1}}^{2}}$-$\frac{1}{{{a}_{n}}^{2}}$=4,
即有$\frac{1}{{{a}_{n}}^{2}}$=1+4(n-1)=4n-3,
由题意可得an=$\frac{1}{\sqrt{4n-3}}$,
$\frac{1}{b_n}=\frac{1}{{{a_{n+1}}}}+\frac{1}{a_n}$=$\frac{4}{\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}}$=$\frac{4}{\sqrt{4n+1}-\sqrt{4n-3}}$,
则bn=$\frac{1}{4}$($\sqrt{4n+1}$-$\sqrt{4n-3}$),
则T20=$\frac{1}{4}$($\sqrt{5}$-1+3-$\sqrt{5}$+$\sqrt{13}$-3+…+9-$\sqrt{77}$)=$\frac{1}{4}$×(9-1)
=2.
故答案为:2.
点评 本题考查数列的求和方法:裂项相消求和,考查等差数列的通项公式的运用,化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | A?B | B. | B?A | C. | A=B | D. | A∩B=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
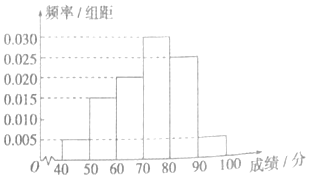
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥4或m≤-2 | B. | m≥2或m≤-4 | C. | -2<m<4 | D. | -4<m<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com