
已知函数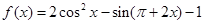 .
.
(1)求函数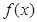 的最小正周期;
的最小正周期;
(2)求函数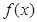 在区间
在区间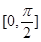 上的最小值和最大值.
上的最小值和最大值.
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:解答题
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C= ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.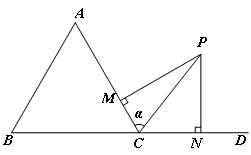
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数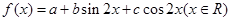 的图像过点
的图像过点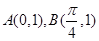 ,且b>0,又
,且b>0,又 的最大值为
的最大值为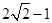 .
.
(1)将 写成含
写成含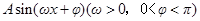 的形式;
的形式;
(2)由函数y = 图像经过平移是否能得到一个奇函数y =
图像经过平移是否能得到一个奇函数y =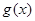 的图像?若能,请写出平移的过程;若不能,请说明理由.
的图像?若能,请写出平移的过程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数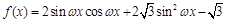 (
(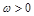 )的最小正周期为
)的最小正周期为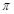 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)将函数 的图象向左平移
的图象向左平移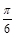 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数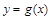 的图象;若
的图象;若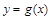 在
在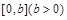 上至少含有10个零点,求b的最小值.
上至少含有10个零点,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为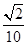 、
、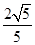 .求:
.求: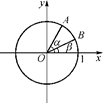
(1) tan(α+β)的值;
(2) α+2β的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com