
����Ŀ����֪����f��x��=x2����a+2��x+alnx�����г���a��0�� ����a��2ʱ������f��x���ĵ����������䣻
�����趨����D�ϵĺ���y=h��x���ڵ�P��x0 �� h��x0�����������߷���Ϊl��y=g��x������ ![]() ��0��D�ں���������PΪ����y=h��x���ġ���ԳƵ㡱����a=4ʱ������y=f��x���Ƿ���ڡ���ԳƵ㡱�������ڣ����������һ������ԳƵ㡱�ĺ����ꣻ�������ڣ���˵�����ɣ�
��0��D�ں���������PΪ����y=h��x���ġ���ԳƵ㡱����a=4ʱ������y=f��x���Ƿ���ڡ���ԳƵ㡱�������ڣ����������һ������ԳƵ㡱�ĺ����ꣻ�������ڣ���˵�����ɣ�
���𰸡��⣺������f��x���Ķ�����Ϊ��0��+�ޣ���
�� ![]() ��
��
�� 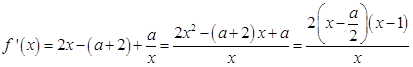
��a��2���� ![]() ��
��
��f�䣨x����0���� 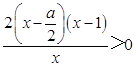 ��
��
��x��0����0��x��1�� ![]() ��
��
���Ժ���f��x���ĵ������������ǣ�0��1���� ![]()
���ⷨһ����a=4ʱ�� ![]()
�����ڵ�P�������߷���Ϊ ![]()
������ ![]() ���ڡ���ԳƵ㡱P��x0��f��x0������
���ڡ���ԳƵ㡱P��x0��f��x0������
��ȼ��ڵ�0��x��x0ʱ��f��x����g��x����
��x��x0ʱ��f��x����g��x���������
�ٵ�0��x��x0ʱ��f��x����g��x���������
�ȼ��� ![]() �������
�������
����0��x��x0ʱ�� ![]() �������
�������
�� ![]() ����գ�x0��=0��
����գ�x0��=0��
Ҫʹ�գ�x0����0��0��x��x0�������ֻҪ�գ�x���ڣ�0��x0�������������ɣ�
�֡� ![]() ��
��
�� ![]() ����
���� ![]() ��
��
�ڵ�x��x0ʱ��f��x����g��x�������ʱ�� ![]() ������10�֣�
������10�֣�
�� ![]() ������11�֣�
������11�֣�
����y=f��x�����ڡ���ԳƵ㡱������һ������ԳƵ㡱�ĺ�����Ϊ ![]() ��
��
���ⷨ����
����y=f��x�����ڡ���ԳƵ㡱������һ������ԳƵ㡱�ĺ�����Ϊ ![]() ���������֤����
���������֤����
�� ![]() ʱ��
ʱ�� ![]()
�ٵ� ![]() ʱ��f��x����g��x���������
ʱ��f��x����g��x���������
�ȼ��� ![]() �������
�������
�� ![]()
�� ![]() ���ຯ���գ�x����
���ຯ���գ�x���� ![]() �ϵ���������
�ϵ���������
�Ӷ��� ![]() ʱ��
ʱ�� ![]() �������
�������
���� ![]() ʱ��f��x����g��x���������
ʱ��f��x����g��x���������
��ͬ���� ![]() ʱ��f��x����g��x���������
ʱ��f��x����g��x���������
����֪y=f��x�����ڡ���ԳƵ㡱������һ������ԳƵ㡱�ĺ�����Ϊ ![]() ��
��
��������������������ĵ��������a�ķ�Χ��������ĵ������伴�ɣ�
����һ��a=4ʱ�����f��x���ĵ������õ����߷��̸����¶�������ȼ��ڵ�0��x��x0ʱ��f��x����g��x������Ϻ����ĵ�����������ɣ�
����������y=f��x�����ڡ���ԳƵ㡱������һ������ԳƵ㡱�ĺ�����Ϊ ![]() ��Ȼ�����֤�����ɣ�
��Ȼ�����֤�����ɣ�


 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ ![]() ��������Ϊ
��������Ϊ ![]() ������ԲC�ϵĵ㵽��Բ�ҽ���F����С����Ϊ
������ԲC�ϵĵ㵽��Բ�ҽ���F����С����Ϊ ![]() .
.
��1������ԲC�ķ��̣�
��2������F�Ҳ���������ƽ�е�ֱ��l����ԲC����A,B���㣬�߶�AB���е�ΪM�� OΪ����ԭ�㣬ֱ�� ![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ ![]() ���ɵȲ����У���ֱ��l�ķ���.
���ɵȲ����У���ֱ��l�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}��ǰn��n��N*�����ΪSn �� a3=3���Ҧ�Sn=anan+1 �� �ڵȱ�����{bn}�У�b1=2�ˣ�b3=a15+1�� ����������{an}��{bn}��ͨ�ʽ��
����������{cn}��ǰn��n��N*�����ΪTn �� �� ![]() ����Tn ��
����Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����DΪ����ʽ��  ����ʾ��ƽ������B��a��b��Ϊ��һ������һ�㣬����������D�ڵ���һ��A��x��y������
����ʾ��ƽ������B��a��b��Ϊ��һ������һ�㣬����������D�ڵ���һ��A��x��y������ ![]() ��������a+b�����ֵ���ڣ� ��
��������a+b�����ֵ���ڣ� ��
A.0
B.1
C.2
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=sin2��x�� ![]() ���أ�0��������Ϊ
���أ�0��������Ϊ ![]() ��������ͼ����x������ƽ��a����λ��a��0��������ͼ�����ԭ��Գƣ���ʵ��a����СֵΪ�� ��
��������ͼ����x������ƽ��a����λ��a��0��������ͼ�����ԭ��Գƣ���ʵ��a����СֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=2 ![]() ��AD=
��AD= ![]() ��MΪDC���е㣬����DAM��AM�۵���D��AM��λ�ã�AD���BM��
��MΪDC���е㣬����DAM��AM�۵���D��AM��λ�ã�AD���BM�� 
��1����֤��ƽ��D��AM��ƽ��ABCM��
��2����EΪD��B���е㣬������E��AM��D�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=xlnx��ax2�ڣ�0��+�ޣ��ϵ����ݼ�����ʵ��a��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() =1��a��b��0������������
=1��a��b��0������������ ![]() ���ҹ���
���ҹ��� ![]() ��ֱ��y=
��ֱ��y= ![]() x+m����ԲC�ཻ��A��B���㣮 ��������ԲC�ķ��̣�
x+m����ԲC�ཻ��A��B���㣮 ��������ԲC�ķ��̣�
�������PAB����������ֵ��
������ֱ��PA��PB�ֱ���y�ύ�ڵ�M��N���ж�|PM|��|PN|�Ĵ�С��ϵ��������֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com