
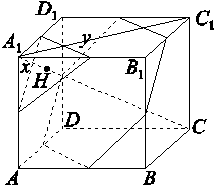
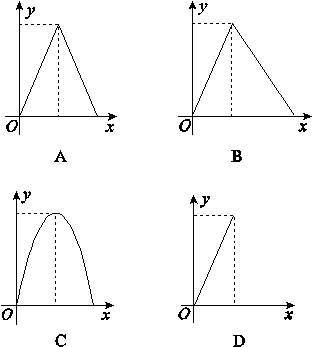
如图,边长为2的正方体A1C中,作对角线A1C的垂面,垂足为H,A1H=x,垂面与上表面相交得到的线段长为y,则y=f(x)的大致图象为( )
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB中点,且△PMB为正三角形.
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
定义在R上的函数g(x)及二次函数h(x)满足:g(x)+2g(-x)=ex+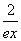 -9,h(-2)=h(0)=1且h(-3)=-2.
-9,h(-2)=h(0)=1且h(-3)=-2.
(1)求g(x)和h(x)的解析式;
(2)对于x1,x2∈[-1,1],均有h(x1)+ax1+5≥g(x2)-x2g(x2)成立,求a的取值范围;
(3)设f(x)=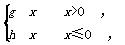 在(2)的条件下,讨论方程f[f(x)]=a+5的解的个数情况.
在(2)的条件下,讨论方程f[f(x)]=a+5的解的个数情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知{an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=a1且bn=an+bn-1(n≥2,n∈N*),求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
在长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )
A.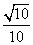 B.
B.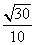 C.
C.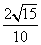 D.
D.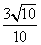
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4,点E,F分别是AB,CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.
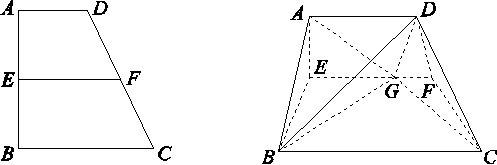
(1)当AG+GC最小时,求证:BD⊥CG;
(2)当2VB-ADGE=VD-GBCF时,求二面角D-BG-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直角坐标系内的两个向量a=(1,3),b=(m,2m-3)使平面内的任意一个向量c都可以唯一地表示成c=λa+μb,则m的取值范围是( )
A.(-∞,0)∪(0,+∞) B.(-∞,-3)∪(-3,+∞)
C.(-∞,3)∪(3,+∞) D.[-3,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知△ABC的三个顶点为A(-1,0),B(1,0),C(3,2),其外接圆为⊙H.
(1)若直线l过点C,且被⊙H截得的弦长为2,求直线l的方程;
(2)对于线段BH上的任意一点P,若在以C为圆心的圆上都存在不同的两点M,N,使得点M是线段PN的中点,求⊙C的半径r的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com