
如图,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4,点E,F分别是AB,CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.
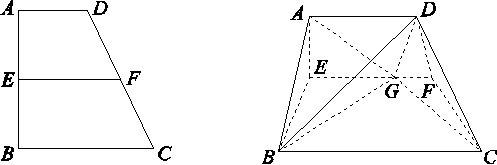
(1)当AG+GC最小时,求证:BD⊥CG;
(2)当2VB-ADGE=VD-GBCF时,求二面角D-BG-C的余弦值.
解:(1)∵点E,F分别是AB,CD的中点,
∴EF∥BC,又∠ABC=90°,
∴AE⊥EF,∵平面AEFD⊥平面EBCF,
∴AE⊥平面EBCF,AE⊥EF,AE⊥BE,又BE⊥EF,
如图,建立空间直角坐标系E-xyz.

翻折前,连接AC交EF于点G,此时点G使得AG+GC最小.
EG= BC=2,又知EA=EB=2,
BC=2,又知EA=EB=2,
则A(0,0,2),B(2,0,0),C(2,4,0),D(0,2,2),
E(0,0,0),G(0,2,0),
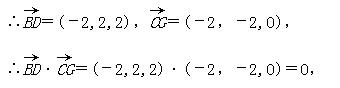 ∴BD⊥CG.
∴BD⊥CG.
(2)设EG=k,
∵AD∥平面EFCB,∴点D到平面EFCB的距离即为点A到平面EFCB的距离.
∵S四边形GBCF= [(3-k)+4]×2=7-k,
[(3-k)+4]×2=7-k,
∴VD-GBCF=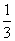 ·S四边形GBCF·AE=
·S四边形GBCF·AE=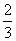 (7-k).
(7-k).
又VB-ADGE=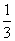 S四边形ADGE·BE=
S四边形ADGE·BE=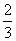 (2+k),
(2+k),
2VB-ADGE=VD-GBCF,∴ (2+k)=
(2+k)=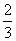 (7-k),
(7-k),
∴k=1,即EG=1.
 ∵所求二面角D-BG-C的平面角为锐角,
∵所求二面角D-BG-C的平面角为锐角,
∴此二面角的余弦值为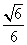 .
.
解法二:过点D作DH⊥EF,垂足为H,过点H作BG延长线的垂线HO,垂足为O,连接OD.
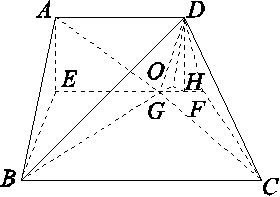
∵平面AEFD⊥平面EBCF,
∴DH⊥平面EBCF,∴OD⊥OB,
∴∠DOH就是二面角D-BG-C的一个平面角.
由于HG=1,在△OHG中,OH=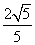 ,
,
又DH=2,在△DOH中,
tan∠DOH=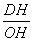 =
=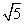 ,
,
∴cos ∠DOH=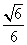 ,
,
∴此二面角的余弦值为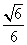 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
已知a,b,c是三个不同的实数.若a,b,c成等差数列,且b,a,c成等比数列,则a∶b∶c=( )
A.2∶1∶4 B.(-2)∶1∶4
C.1∶2∶4 D.1∶(-2)∶4
查看答案和解析>>
科目:高中数学 来源: 题型:
春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
|
| 做不到“光盘” | 能做到“光盘” |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
附: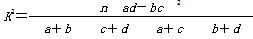 其中n=a+b+c+d为样本容量.
其中n=a+b+c+d为样本容量.
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com