练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知a，b，c是三个不同的实数．若a，b，c成等差数列，且b，a，c成等比数列，则a∶b∶c＝(　　)

    A．2∶1∶4                              B．(－2)∶1∶4 

    C．1∶2∶4                              D．1∶(－2)∶4


    B

    [解析]　依题意有检验各选项，可知B正确．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在中 ，角A、B、C的对边分别为，。

    求角A的大小；

    （2）若，求c的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知，且//(),则k=______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设直线x＝t与函数f(x)＝x2＋1，g(x)＝x＋ln x的图象分别交于P，Q两点，则|PQ|的最小值是(　　)

    A．－     B.  C．1     D．－或1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义在R上的函数g(x)及二次函数h(x)满足：g(x)＋2g(－x)＝ex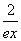＋－9，h(－2)＝h(0)＝1且h(－3)＝－2.

    (1)求g(x)和h(x)的解析式；

    (2)对于x1，x2∈[－1,1]，均有h(x1)＋ax1＋5≥g(x2)－x2g(x2)成立，求a的取值范围；

    (3)设f(x)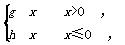＝在(2)的条件下，讨论方程f[f(x)]＝a＋5的解的个数情况．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}的首项为3，{bn}为等差数列，且bn＝an＋1－an(n∈N*)，若b3＝－2，b10＝12，则a8＝(　　)

    A．0                                    B．3 

    C．8                                    D．11

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知{an}是一个公差大于0的等差数列，且满足a3a6＝55，a2＋a7＝16.

    (1)求数列{an}的通项公式；

    (2)若数列{bn}满足b1＝a1且bn＝an＋bn－1(n≥2，n∈N*)，求数列{bn}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，直角梯形ABCD中，∠ABC＝90°，AB＝BC＝2AD＝4，点E，F分别是AB，CD的中点，点G在EF上，沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF.

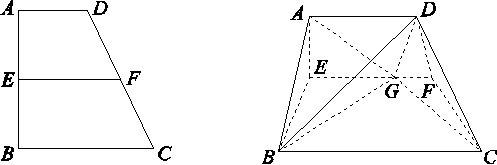
    (1)当AG＋GC最小时，求证：BD⊥CG；

    (2)当2VB－ADGE＝VD－GBCF时，求二面角D－BG－C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设△ABC内角A，B，C的对边分别为a，b，c，且满足ccos B－bcos C＝a，则＝________.

    查看答案和解析>>

    同步练习册答案