
分析 构造新的函数,将f(x)转化为可以知道性质的函数,将x0的范围确定出来,再处理g(x),由性质确定出a的范围.
解答 解:∵f(-x)+f(x)=x2
∴令F(x)=f(x)-$\frac{1}{2}{x}^{2}$,
∴f(x)-$\frac{1}{2}{x}^{2}$=-f(-x)+$\frac{1}{2}$x2
∴F(x)=-F(-x),即F(x)为奇函数,
∵F′(x)=f′(x)-x,
且当x<0时,f′(x)<x,
∴F′(x)<0对x<0恒成立,
∵F(x)为奇函数,
∴F(x)在R上单调递减,
∵f(x)+$\frac{1}{2}$≥f(1-x)+x,
∴f(x)+$\frac{1}{2}$-$\frac{1}{2}{x}^{2}$≥f(1-x)+x-$\frac{1}{2}{x}^{2}$,
即F(x)≥F(1-x),
∴x≤1-x,
x0≤$\frac{1}{2}$,
由g[g(x0)]=x0可得g(x0)=g-1(x0),
而g(x)如果与其反函数相交,则交点一定在直线y=x上,
故有g(x0)=x0,
即h(x)=ex+x-a=0在(-∞,$\frac{1}{2}$]有解.
∵h′(x)=ex+1,
∴h(x)在R上单调递增.
∴h(x)max=h($\frac{1}{2}$)=$\sqrt{e}$+$\frac{1}{2}$-a≥0即可,
∴a≤$\sqrt{e}$+$\frac{1}{2}$.
点评 本题考查对f(x)那个式子的处理,重新构造新的函数,通过新函数确定x0的范围,再来确定a的范围.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln2+1 | B. | ln2-1 | C. | ln3+1 | D. | ln3-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
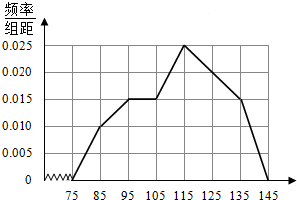 某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )
某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )| A. | 100 | B. | 110 | C. | 115 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{0}$ | B. | $\overrightarrow{PC}$+$\overrightarrow{PA}$=$\overrightarrow{0}$ | C. | $\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$ | D. | $\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com