
分析 (1)根据平面上两点间的距离公式写出|AB|的表达式;
(2)根据题意,利用AB=$\frac{1}{2}$AC得出$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AC}$,列出方程求出点C的坐标;
(3)求出f(x)的解析式并化简,根据x的取值范围求出f(x)的值域,得出m、n的取值范围,再求n-m的最小值.
解答 解:(1)AB之间的距离为|AB|=$\sqrt{{{(x}_{1}{-x}_{2})}^{2}{+{(y}_{1}{-y}_{2})}^{2}}$;
(2)∵点C在AB的延长线上,满足AB=$\frac{1}{2}$AC,
∴$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AC}$,
又$\overrightarrow{AB}$=(-2,4),$\overrightarrow{AC}$=(x0-2,y0),
∴$\left\{\begin{array}{l}{-2=\frac{1}{2}{(x}_{0}-2)}\\{4={\frac{1}{2}y}_{0}}\end{array}\right.$,
解得x0=-2,y0=8,
∴点C的坐标为(-2,8);
(3)∵x1=2cos(x-$\frac{π}{6}$),x2=1,y1=0,y2=sin(x-$\frac{π}{6}$),
∴f(x)=|$\overrightarrow{AB}$|2=${[2cos(x-\frac{π}{6})-1]}^{2}$+sin2(x-$\frac{π}{6}$)
=${[-{2sin}^{2}\frac{1}{2}(x-\frac{π}{6})]}^{2}$+22sin2$\frac{1}{2}$(x-$\frac{π}{6}$)cos2$\frac{1}{2}$(x-$\frac{π}{2}$)
=4sin2($\frac{1}{2}$x-$\frac{π}{12}$)
=2[1-cos(x-$\frac{π}{6}$)]
=2-2cos(x-$\frac{π}{6}$);
又x∈[0,$\frac{π}{2}$],∴x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{π}{3}$],
∴cos(x-$\frac{π}{6}$)∈[$\frac{1}{2}$,1],
∴-2cos(x-$\frac{π}{6}$)∈[-2,-1],
∴2-2cos(x-$\frac{π}{6}$)∈[0,1],
即f(x)∈[0,1];
又f(x)∈[m,n],
∴m≤0且n≥1,
∴n-m的最小值为1-0=1.
点评 本题考查了平面向量的坐标运算与应用问题,也考查了两点间的距离公式以及三角函数的最值问题,是综合性题目.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)在[a,b]上可导 | |
| B. | ${∫}_{a}^{x}$f(t)dt为f(x)在[a,b]上的一个原函数: | |
| C. | ${∫}_{x}^{b}$f(t)dt为f(x)在[a,b]上的一个原函数 | |
| D. | f(x)在[a,b]上至少有一个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
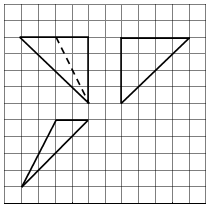
| A. | 8+8$\sqrt{2}$+4$\sqrt{6}$ | B. | 8+8$\sqrt{2}$+2$\sqrt{6}$ | C. | 2+2$\sqrt{2}$+$\sqrt{6}$ | D. | $\frac{1}{2}$+$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四边形ABCD是矩形,AB=1,AD=2,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.
已知四边形ABCD是矩形,AB=1,AD=2,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com