
 抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.
抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.分析 (1)根据抛物线方程求得抛物线的焦点坐标,进而根据点斜式求得直线的方程与抛物线方程联立,消去y,根据韦达定理求得x1+x2=的值,进而根据抛物线的定义可知|AB|=x1+$\frac{p}{2}$+x2+$\frac{p}{2}$=x1+x2+p,求得答案.
(2)过A,B做准线的垂线,垂足分别为P,Q,则|AP|=|AF|,|BQ|=|BF|,得出以AB为直径的圆M与准线相切于H,即可得出结论.
解答 解:(1)抛物线焦点为(1,0),且斜率为1,
则直线方程为y=x-1,代入抛物线方程y2=4x得
x2-6x+1=0,设A(x1,y1),B(x2,y2)
∴x1+x2=6
根据抛物线的定义可知|AB|=x1+$\frac{p}{2}$+x2+$\frac{p}{2}$=x1+x2+p=6+2=8;
(2)过A,B做准线的垂线,垂足分别为P,Q,则|AP|=|AF|,|BQ|=|BF|,
∴|AB|=|AF|+|BF|=|AP|+|BQ|,
∵M是AB的中点,
∴|MH|=$\frac{|AP|+|BQ|}{2}$=4,
∴以AB为直径的圆M与准线相切于H,
∴∠AHB=90°.
点评 本题主要考查了直线与圆锥曲线的关系,抛物线的简单性质.关键是:将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系,利用弦长公式即可求得|AB|值,从而解决问题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 2π,[$\frac{3π}{8}$,$\frac{7π}{8}$] | B. | π,[$\frac{3π}{8}$,$\frac{7π}{8}$] | C. | 2π,[-$\frac{π}{8}$,$\frac{3π}{8}$] | D. | π,[-$\frac{π}{8}$,$\frac{3π}{8}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| y | 2.4 | 4.5 | 4.6 | 6.5 |
| A. | 2.4 | B. | 2.84 | C. | 3.67 | D. | 3.95 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有唯一的解 | B. | 有无穷多解 | ||
| C. | 由m的值决定解的情况 | D. | 无解 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知F1、F2分别为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上、下焦点,其中F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.
已知F1、F2分别为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上、下焦点,其中F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
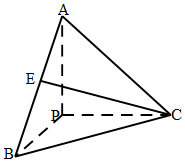 已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.
已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com