
分析 (1)由绝对值不等式的解法求出集合A,把a=1代入不等式,由分式不等式、一元二次不等式的解法求出集合B,由并集的运算求出A∪B;
(2)由条件可得A⊆B,将分式不等式转化后,对a分类讨论,分别由子集的定义,求出实数a的取值范围.
解答 解:(1)由|x-1|≤1得-1≤x-1≤1,解得0≤x≤2,
则集合A=[0,2],
当a=1时,不等式$\frac{x-a}{x+1}<0$化为(x+1)(x-1)<0,
解得-1<x<1,则B=(-1,1),
∴A∪B=(-1,2];
(2)∵对于任意的实数x0∈A,都有x0∈B,
∴A⊆B,即[0,2]⊆B,
不等式$\frac{x-a}{x+1}<0$化为(x+1)(x-a)<0,
①当a≤-1时,不满足A⊆B;
②当a>-1时,集合B=(-1,a),
∵[0,2]⊆(-1,a),∴a>2,
∴实数a的取值范围是(2,+∞).
点评 本题考查绝对值不等式、分式不等式的等价转化及解法,一元二次不等式的解法,考查分类讨论思想,转化思想,化简、变形能力.


科目:高中数学 来源: 题型:选择题
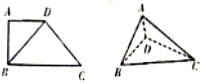 如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )| A. | 平面ABD⊥平面ABC | B. | 平面ACD⊥平面BCD | C. | 平面ABC⊥平面BCD | D. | 平面ACD⊥平面ABC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4<m<5 | B. | 3<m<5 | C. | 1<m<5 | D. | 1<m<3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.
抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -2 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com