
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
分析 由已知利用三角形面积公式,余弦定理,同角三角函数基本关系式化简可求tanA=2,进而利用三角形内角和定理,两角和的正切函数公式化简整理即可得解.
解答 解:∵$S=\frac{1}{2}({b^2}+{c^2}-{a^2})$,
∴$\frac{1}{2}$bcsinA=$\frac{1}{2}$×2bccosA,解得:tanA=2,
∴tanA=-tan(B+C)=-$\frac{tanB+tanC}{1-tanBtanC}$=2,整理可得:tanB+tanC-2tanBtanC=-2,
故选:D.
点评 本题主要考查了三角形面积公式,余弦定理,同角三角函数基本关系式,三角形内角和定理,两角和的正切函数公式在解三角形中的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 70尺 | B. | 80尺 | C. | 90尺 | D. | 100尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π,[$\frac{3π}{8}$,$\frac{7π}{8}$] | B. | π,[$\frac{3π}{8}$,$\frac{7π}{8}$] | C. | 2π,[-$\frac{π}{8}$,$\frac{3π}{8}$] | D. | π,[-$\frac{π}{8}$,$\frac{3π}{8}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
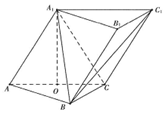 在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.
在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 87 | B. | 88 | C. | 89 | D. | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有唯一的解 | B. | 有无穷多解 | ||
| C. | 由m的值决定解的情况 | D. | 无解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com