
| A. | 2π,[$\frac{3π}{8}$,$\frac{7π}{8}$] | B. | π,[$\frac{3π}{8}$,$\frac{7π}{8}$] | C. | 2π,[-$\frac{π}{8}$,$\frac{3π}{8}$] | D. | π,[-$\frac{π}{8}$,$\frac{3π}{8}$] |
分析 将f(x)化简,结合三角函数的性质求解即可.
解答 解:由f(x)=2sin2x+2sinxcosx=sin2x-cos2x+1=$\sqrt{2}$sin(2x-$\frac{π}{4}$)+1
∴f(x)的最小正周期T=$\frac{2π}{2}=π$,
由$\frac{π}{2}+2kπ≤2x-\frac{π}{4}≤\frac{3π}{2}+2kπ$单调递减,
解得:$\frac{3π}{8}+kπ≤x≤\frac{7π}{8}+kπ$,(k∈Z)
当k=0时,得f(x)的一个单调减区间[$\frac{3π}{8}$,$\frac{7π}{8}$].
故选B.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.


科目:高中数学 来源: 题型:选择题
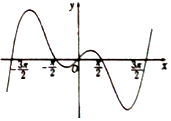
| A. | f(x)=x+sinx | B. | f(x)=$\frac{cosx}{x}$ | C. | f(x)=x(x-$\frac{π}{2}$)(x-$\frac{3π}{2}$) | D. | f(x)=xcosx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
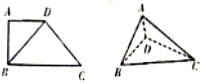 如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )| A. | 平面ABD⊥平面ABC | B. | 平面ACD⊥平面BCD | C. | 平面ABC⊥平面BCD | D. | 平面ACD⊥平面ABC |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 报考“经济类” | 不报“经济类” | 合计 | |
| 男 | 6 | 24 | 30 |
| 女 | 14 | 6 | 20 |
| 合计 | 20 | 30 | 50 |
| P(X2≥k) | 0.05 | 0.010 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4<m<5 | B. | 3<m<5 | C. | 1<m<5 | D. | 1<m<3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.
抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com