
| A. | 1 | B. | 0 | C. | -2 | D. | -1 |
分析 由“函数$f(x)={(\frac{1}{3})^x}+m-\frac{1}{3}$的图象不过第三象限”,可得$m-\frac{1}{3}$≥0,解得m$≥\frac{1}{3}$.即可得出.
解答 解:由“函数$f(x)={(\frac{1}{3})^x}+m-\frac{1}{3}$的图象不过第三象限”,可得$m-\frac{1}{3}$≥0,解得m$≥\frac{1}{3}$.
∵“m>a”是“函数$f(x)={(\frac{1}{3})^x}+m-\frac{1}{3}$的图象不过第三象限”的必要不充分条件,
∴实数a能取的最大整数为-1.
故选:D.
点评 本题考查了函数的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有唯一的解 | B. | 有无穷多解 | ||
| C. | 由m的值决定解的情况 | D. | 无解 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知F1、F2分别为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上、下焦点,其中F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.
已知F1、F2分别为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上、下焦点,其中F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
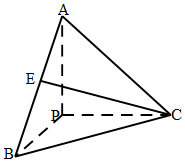 已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.
已知如图,PA、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面PAC所成角的正弦值为$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {5,7} | B. | {1,3,9} | C. | {3,5,7} | D. | {1,2,3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com