
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 (1)根据几何概型的概率公式进行计算.
(2)根据充分条件和必要条件的定义进行判断.
(3)根据面面垂直的判定定理进行判断.
(4)根据向量的有关概念和性质分别判断p,q的真假,利用复合命题之间的关系即可得到结论.
解答 解:(1)由3a-1>0得a>$\frac{1}{3}$,∵0≤a≤1,∴事件“3a-1>0”发生的概率P=$\frac{1-\frac{1}{3}}{1-0}$=$\frac{2}{3}$,故(1)错误,
(2))“x+y≠0”是“x≠1或y≠-1”的逆否命题为:若x=1且y=-1,则x+y=0,
则x=1且y=-1,是x+y=0成立的充分不必要条件,故)“x+y≠0”是“x≠1或y≠-1”的充分不必要条件,故(2)正确,
(3)如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β的逆否命题是:
平面α内存在直线垂直于平面β,则平面α垂直于平面β,则逆否命题为真命题,
则原命题为真命题,故(3)正确,
(4)若$\overrightarrow{a}$•$\overrightarrow{b}$=0,$\overrightarrow{b}$•$\overrightarrow{c}$=0,则$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$•$\overrightarrow{c}$,即($\overrightarrow{a}$-$\overrightarrow{c}$)•$\overrightarrow{b}$=0,则$\overrightarrow{a}$•$\overrightarrow{c}$=0不一定成立,故命题p为假命题,
若$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{b}$∥$\overrightarrow{c}$,则$\overrightarrow{a}$∥$\overrightarrow{c}$平行,故命题q为真命题,则“p∨q”是真命题为真命题.,故(4)正确,
故正确的是(2)(3)(4),共有3个,
故选:C
点评 本题主要考查命题的真假判断,涉及几何概型,充分条件和必要条件以及复合命题的真假判断,知识点较多,综合性较强,但难度不大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $80\sqrt{5}$ | B. | $60\sqrt{5}$ | C. | $40\sqrt{5}$ | D. | $20\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
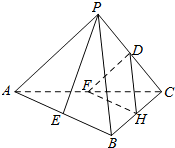 如图,在三棱锥P-ABC中,E、F、G、H分别是AB、AC、PC、BC的中点,且PA=PB,AC=BC.
如图,在三棱锥P-ABC中,E、F、G、H分别是AB、AC、PC、BC的中点,且PA=PB,AC=BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com