
分析 根据函数的单调性判断出p为真时m的范围,根据复数的意义判断出q为真时m的范围,取交集即可.
解答 解:p:∵函数f(x)=$\frac{1}{3}$x3-(4m-1)x2+(15m2-2m-7)x+2在R上是增函数,
∴f′(x)=x2-(8m-2)x+15m2-2m-7≥0恒成立,
∴△=(8m-2)2-4(15m2-2m-7)≤0,解得:2≤m≤4
∴p为真时:2≤m≤4;
q:复数z=(m2+m+1)+(m2-3m)i,m∈R表示的点位于复平面第四象限,
∴$\left\{\begin{array}{l}{{m}^{2}+m+1>0}\\{{m}^{2}-3m<0}\end{array}\right.$,解得:0<m<3,
∴q为真时:0<m<3,
∴P真q真时:$\left\{\begin{array}{l}{2≤m≤4}\\{0<m<3}\end{array}\right.$,
∴2≤m<3.
点评 本题考查了复合命题的判断,考查函数的单调性问题,复数问题,是一道基础题.


科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [-1,1] | C. | (-1,0] | D. | [0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
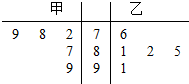 将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )
将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )| A. | x甲<x乙,乙比甲成绩稳定 | B. | x甲>x乙;甲比乙成绩稳定 | ||
| C. | x甲>x乙;乙比甲成绩稳定 | D. | x甲<x乙;甲比乙成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
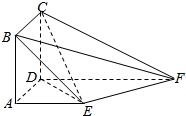 如图,四边形ABCD为正方形,四边形AEFD为梯形,FD∥EA,FD⊥平面ABCD,FD=2EA=2AD.
如图,四边形ABCD为正方形,四边形AEFD为梯形,FD∥EA,FD⊥平面ABCD,FD=2EA=2AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab<ba<logab | B. | ba<logab<ab | C. | logab<ba<ab | D. | logab<ab<ba |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
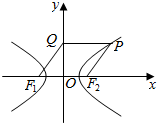 已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )
已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )| A. | $\frac{1+\sqrt{2}}{2}$ | B. | $\frac{1+\sqrt{3}}{2}$ | C. | 1$+\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com