【题目】如图①，在平行四边形
中，
，
，
，
为
中点.将
沿
折起使平面
平面
，得到如图②所示的四棱锥
.
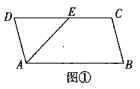
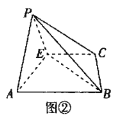
（1）求证：平面
平面
；
（2）求直线
与平面
所成角的正弦值.
【答案】（1）证明见解析（2）
【解析】
（1）利用勾股定理求得
，即可由面面垂直推证线面垂直，再由线面垂直推证面面垂直；
（2）以
为坐标原点，建立空间直角坐标系，求得
的方向向量，以及平面
的法向量，即可容易求得线面角.
（1）证明：在图①中连接
，
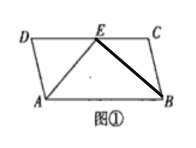
因为
，
，
，为
中点，
故可得
为等边三角形，故可得
；
在
中，由余弦定理可得
，解得
.
又
，故可得
.
，
在图②中，
平面
平面
，且平面
平面
，
平面
，
又
平面
，
平面
平面.
（2）以为坐标原点，
为
轴，
为
轴，
过点垂直于平面的直线为
轴，建立如图所示的空间直角坐标系，
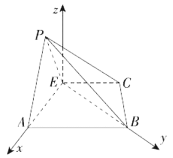
则
，
，
，
，
，
故可得
.
设平面
的一个法向量
，
由
，
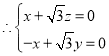，令
，
可得
，
设直线
与平面所成角的正弦值为
，
则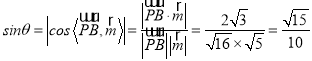
.
直线与平面所成角的正弦值为.
超能学典应用题题卡系列答案科目：高中数学 来源： 题型：
【题目】2020年春节期间，因新冠肺炎疫情防控工作需要，
、
两社区需要招募义务宣传员，现有
、
、
、
、
、
六位大学生和甲、乙、丙三位党员教师志愿参加，现将他们分成两个小组分别派往、两社区开展疫情防控宣传工作，要求每个社区都至少安排1位党员教师及3位大学生，且由于工作原因只能派往社区，则不同的选派方案种数为（ ）
A.60B.90
C.120D.150
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2019年1月1日，济南轨道交通
号线试运行，济南轨道交通集团面向广大市民开展“参观体验，征求意见”活动，市民可以通过济南地铁APP抢票，小陈抢到了三张体验票，准备从四位朋友小王，小张，小刘，小李中随机选择两位与自己一起去参加体验活动，则小王被选中的概率为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，椭圆
：
（
）和圆
：
，已知圆将椭圆的长轴三等分，椭圆右焦点到右准线的距离为
，椭圆的下顶点为
，过坐标原点
且与坐标轴不重合的任意直线
与圆相交于点
、
．
（1）求椭圆的方程；
（2）若直线
、
分别与椭圆相交于另一个交点为点
、
.
①求证：直线
经过一定点；
②试问：是否存在以
为圆心，
为半径的圆
，使得直线
和直线
都与圆相交？若存在，请求出实数
的范围；若不存在，请说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知椭圆
的左右顶点分别是
，离心率为
，设点
，连接
交椭圆于点
，坐标原点是
．
（1）证明： 
；
（2）设三角形
的面积为
，四边形
的面积为
， 若 
的最小值为1，求椭圆的标准方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数f（x）＝sinωx（ω＞0）的图象与其对称轴在y轴右侧的交点从左到右依次记为A1，A2，A3，…，An，…，在点列{An}中存在三个不同的点Ak、Al、Ap，使得△AkAlAp是等腰直角三角形，将满足上述条件的ω值从小到大组成的数记为ωn，则ω6＝_____．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，底面
为梯形，
，若棱
，
，
两两垂直，长度分别为1，2，2，且向量
与
夹角的余弦值为
.
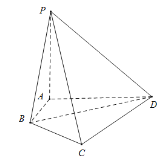
（1）求
的长度；
（2）求直线
与平面
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
