
已知 为常数,且
为常数,且 ,函数
,函数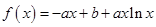 ,
,
( 是自然对数的底数).
是自然对数的底数).
(1)求实数 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)当 时,是否同时存在实数
时,是否同时存在实数 和
和 (
( ),使得对每一个
),使得对每一个 ,直线
,直线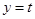 与曲线
与曲线
 都有公共点?若存在,求出最小的实数
都有公共点?若存在,求出最小的实数 和最大的实数
和最大的实数 ;若不存在,说明理由.
;若不存在,说明理由.
(1) ;(2)当
;(2)当 时,
时, 的单调增区间为
的单调增区间为 ,单调减区间为
,单调减区间为 ,当
,当 时,
时, 的单调增区间为
的单调增区间为 ,单调减区间为
,单调减区间为 ;(3) 当
;(3) 当 时,存在实数
时,存在实数 和
和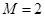 ,使得对每一个
,使得对每一个 ,直线
,直线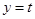 与曲线
与曲线
 都有公共点,可得
都有公共点,可得 .
.
解析试题分析:(1) 由
科目:高中数学
来源:
题型:解答题
对于三次函数
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
已知函数f(x)=
科目:高中数学
来源:
题型:解答题
修建一个面积为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 可解得
可解得 的值;(2)对函数求导可得
的值;(2)对函数求导可得 ,对
,对 进行讨论,解
进行讨论,解 ,
, 分别可得单调递增与递减区间;(3)当
分别可得单调递增与递减区间;(3)当 时,
时, ,求出导数判断
,求出导数判断 在
在 的变化情况,得
的变化情况,得 在区间
在区间 内值域为
内值域为 ,假设存在题目中要求的点,那么每一个
,假设存在题目中要求的点,那么每一个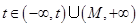 ,直线
,直线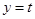 与曲线
与曲线
 都没有公共点.
都没有公共点.
解: (1)由 ,得
,得 ; 2分
; 2分
(2)由(Ⅰ), .定义域为
.定义域为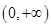 . .3分
. .3分
从而 , ..4分
, ..4分
因为 ,所以
,所以
当 时,由
时,由 得
得 ,由
,由 得
得 ;5分
;5分
当 时,由
时,由 得
得 ,由
,由 得
得 ;6分
;6分
因而, 当 时,
时, 的单调增区间为
的单调增区间为 ,单调减区间为
,单调减区间为 , ..7分
, ..7分
当 时,
时, 的单调增区间为
的单调增区间为 ,单调减区间为
,单调减区间为 . .8分
. .8分
(3)当 时,
时, .
. .令
.令 ,则
,则 .
.
当 在区间
在区间 内变化时,
内变化时, ,
, 的变化情况如下表:
的变化情况如下表:






黄冈小状元作业本系列答案
课时达标练与测系列答案

经纶学典课时作业系列答案




浙江名卷系列答案
励耘活页系列答案

 。
。
定义:(1)设 是函数
是函数 的导数
的导数 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”;
的“拐点”;
定义:(2)设 为常数,若定义在
为常数,若定义在 上的函数
上的函数 对于定义域内的一切实数
对于定义域内的一切实数 ,都有
,都有 成立,则函数
成立,则函数 的图象关于点
的图象关于点 对称。
对称。
己知 ,请回答下列问题:
,请回答下列问题:
(1)求函数 的“拐点”
的“拐点” 的坐标
的坐标
(2)检验函数 的图象是否关于“拐点”
的图象是否关于“拐点” 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数 ,使得它的“拐点”是
,使得它的“拐点”是 (不要过程)
(不要过程) ,(
,(  为常数,
为常数, 为自然对数的底).
为自然对数的底).
(1)当 时,求
时,求 ;
;
(2)若 在
在 时取得极小值,试确定
时取得极小值,试确定 的取值范围;
的取值范围;
(3)在(2)的条件下,设由 的极大值构成的函数为
的极大值构成的函数为 ,将
,将 换元为
换元为 ,试判断曲线
,试判断曲线 是否能与直线
是否能与直线 (
( 为确定的常数)相切,并说明理由.
为确定的常数)相切,并说明理由. (a∈R).
(a∈R).
(1)求f(x)的极值;
(2)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围. 平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为
平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为 元.
元.
(1)求 的表达式;
的表达式;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号