Question

13．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{1+9{x}^{2}，}}&{x≤0}\\{1+x{e}^{x-1}，}&{x＞0}\end{array}\right.$，点A、B是函数f（x）图象上不同两点，则∠AOB（O为坐标原点）的取值范围是（　　）

• A． （0，$\frac{π}{4}$）
• B． （0，$\frac{π}{4}$]
• C． （0，$\frac{π}{3}$）
• D． （0，$\frac{π}{3}$]

Answer 1

分析 当x≤0时，函数f（x）是双曲线得到渐近线的斜率k=-3，当x＞0时，求函数过原点的切线，根据直线的夹角公式进行求解即可．

解答 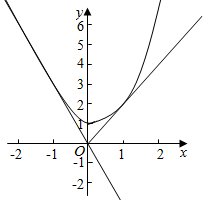解：当x≤0时，由y=$\sqrt{1+9{x}^{2}}$得y²-9x²=1，（x≤0），此时对应的曲线为双曲线，双曲线的渐近线为y=-3x，此时渐近线的斜率k₁=-3，
当x＞0时，f（x）=1+xe^x-1，当过原点的直线和f（x）相切时，设切点为（a，1+ae^a-1），
函数的导数f′（x）=e^x-1+xe^x-1=（x+1）e^x-1，
则切线斜率k₂=f′（a）=（a+1）e^a-1，
则对应的切线方程为y-（1+ae^a-1）=（1+a）e^a-1（x-a），
即y=（1+a）e^a-1（x-a）+1+ae^a-1，
当x=0，y=0时，（1+a）e^a-1（-a）+1+ae^a-1=0，
即a²e^a-1+ae^a-1=1+ae^a-1，
即a²e^a-1=1，得a=1，此时切线斜率k₂=2，
则切线和y=-3x的夹角为θ，
则tanθ=|$\frac{-3-2}{1-2×3}$|=$\frac{5}{5}=1$，则θ=$\frac{π}{4}$，
故∠AOB（O为坐标原点）的取值范围是（0，$\frac{π}{4}$），
故选：A．

点评 本题主要考查直线夹角的求解，根据双曲线的渐近线和导数的几何意义求出切线斜率是解决本题的关键．综合性较强，有一定的难度．