
分析 求A点到C1的最短距离,由两点之间直线段最短,想到需要把长方体剪开再展开,把A到C1的最短距离转化为求三角形的边长问题,根据实际图形,应该有三种展法,展开后利用勾股定理求出每一种情况中AC1的长度,比较三个值的大小后即可得到结论.
解答 解:长方体ABCD-A1B1C1D1的表面可有三种不同的方法展开,
如图所示.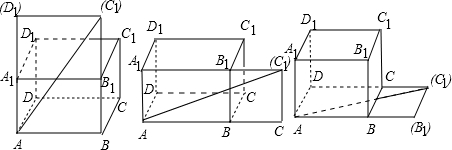 ,
,
AB=1,BC=2,BB1=3.
表面展开后,依第一个图形展开,AC1=$\sqrt{(3+2)^{2}+{1}^{2}}$=$\sqrt{26}$.
依第二个图形展开,AC1=$\sqrt{(1+2)^{2}+{3}^{2}}$=3$\sqrt{2}$.
依第三个图形展开,AC1=$\sqrt{(3+1)^{2}+{2}^{2}}$=2$\sqrt{5}$.
三者比较,得A点沿长方形表面到C1的最最小值为$3\sqrt{2}$.
故答案为:$3\sqrt{2}$.
点评 本题考查了点、线、面之间的距离,考查了学生的空间想象能力和思维能力,考查了数学转化思想方法,解答的关键是想到对长方体的三种展法,是中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{16}$ | B. | $\frac{1}{4}$ | C. | $-\frac{9}{16}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2x | B. | f(x)=lnx | C. | $f(x)=\frac{1}{x}$ | D. | $f(x)={log_{\frac{1}{3}}}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | (-∞,3) | C. | (3,+∞) | D. | [2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{1}{4})$ | B. | $(-\frac{1}{4},0)$ | C. | $(-\frac{1}{4},0]$ | D. | $[-\frac{1}{4},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
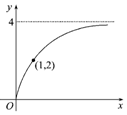
| A. | y=2$\sqrt{x}$ | B. | y=log3(x+1) | C. | y=4-$\frac{4}{x+1}$ | D. | y=$\root{3}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com