
【题目】关于![]() 的函数
的函数![]() .
.
(Ⅰ)若![]() 为单调函数,试求实数
为单调函数,试求实数![]() 的取值范围;
的取值范围;
(Ⅱ)讨论![]() 的零点个数.
的零点个数.
【答案】(1)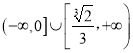 (2)见解析
(2)见解析
【解析】试题分析:(1)分两种情况, ![]() 时,
时, ![]() 时,分别求导研究函数的单调性;(2)结合第一问的单调性,和函数图像,从三方面来考虑函数的变化趋势
时,分别求导研究函数的单调性;(2)结合第一问的单调性,和函数图像,从三方面来考虑函数的变化趋势![]() 或
或![]() ,
, ![]() ,
, ![]() 或
或![]() 时。
时。
解析:
(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,
![]()
①![]() 时,
时, ![]() 恒成立,故
恒成立,故![]() 为单调递增函数.
为单调递增函数.
②![]() 时,令
时,令![]() ,
,
![]() .
.
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴![]() 为
为![]() 的极大值点,也是
的极大值点,也是![]() 上的最大值点.
上的最大值点.
若![]() ,得
,得![]()
∴![]() 时,
时, ![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上单调递减.
上单调递减.
综上,若![]() 为单调函数,实数
为单调函数,实数![]() 的取值范围是
的取值范围是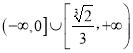 .
.
若使用变量分离法,参照标准给分.
(Ⅱ)由题设知, ![]() ,
,
①由(Ⅰ)知, ![]() 或
或![]() 时,
时, ![]() 单调,故
单调,故![]() 只一个零点.
只一个零点.
②若![]() 得
得![]() 得
得![]() ,
,
则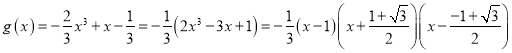 .
.
当![]() 或
或![]() 时
时![]() ,即
,即![]() ,
,
当![]() 时
时![]() .即
.即![]() .
.
![]() 在
在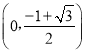 和
和![]() 上单调递减,在
上单调递减,在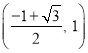 上单调递增,
上单调递增,
∴![]() 的极小值点
的极小值点![]() ,极大值点
,极大值点![]() .
.
又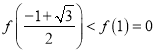 ,
,
根据函数的增长速度, ![]() 时
时![]() ,
, ![]() 时
时![]() ,
,
∴![]() 有两个零点,一个在区间
有两个零点,一个在区间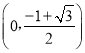 ,另一个为
,另一个为![]() .
.
③![]() 或
或![]() 时,有
时,有![]() .
.
又![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
且![]() ,
, ![]() 时
时![]() ,
,
故必存在不为1的![]() ,
, ![]() ,使得
,使得![]() ,
,
故![]() 时,
时, ![]() ,则
,则![]() ;
; ![]() 时,
时, ![]() ,则
,则![]() .
.
∴![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() 时,
时, ![]() ,故
,故![]() ,由
,由![]() 及
及![]() 时
时![]() ,
, ![]() 时
时![]() 知,
知, ![]() 有三个零点.
有三个零点.
![]() 时,
时,
∵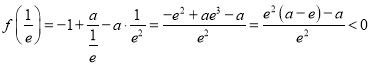 .
.
![]() ,即
,即![]() ,
,
∴必有![]() 且
且![]() ,
, ![]() .
.
又![]() 时
时![]() ,
, ![]() 时
时![]() ,
,
故![]() 有三个零点.
有三个零点.
综上, ![]() 或
或![]() 等时,
等时, ![]() 只一个零点;
只一个零点; ![]() 时,
时, ![]() 有两个零点;
有两个零点; ![]() 或
或![]() 时,
时, ![]() 有三个零点.
有三个零点.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】某省为了确定合理的阶梯电价分档方案,对全省居民用量进行了一次抽样调查,得到居民月用电量(单位:度)的频率分布直方图(如图所示),求:
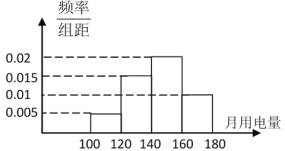
(1)若要求80%的居民能按基本档的电量收费,则基本档的月用电量应定为多少度?
(2)由频率分布直方图可估计,居民月用电量的众数、中位数和平均数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 和
和![]() 是椭圆
是椭圆![]() 的两个焦点,且点
的两个焦点,且点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)直线![]() (m>0)与椭圆C有且仅有一个公共点,且与x轴和y轴分别交于点M,N,当△OMN面积取最小值时,求此时直线
(m>0)与椭圆C有且仅有一个公共点,且与x轴和y轴分别交于点M,N,当△OMN面积取最小值时,求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月16日摩拜单车进驻大连市旅顺口区,绿色出行引领时尚,旅顺口区对市民进行“经常使用共享单车与年龄关系”的调查统计,若将单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,抽取一个容量为200的样本,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”。使用次数为5次或不足5次的称为“不常使用单车用户”,已知“经常使用单车用户”有120人,其中![]() 是“年轻人”,已知“不常使用单车用户”中有
是“年轻人”,已知“不常使用单车用户”中有![]() 是“年轻人”.
是“年轻人”.
(1)请你根据已知的数据,填写下列![]() 列联表:
列联表:
年轻人 | 非年轻人 | 合计 | |
经常使用单车用户 | |||
不常使用单车用户 | |||
合计 |
(2)请根据(1)中的列联表,计算![]() 值并判断能否有
值并判断能否有![]() 的把握认为经常使用共享单车与年龄有关?
的把握认为经常使用共享单车与年龄有关?
(附: 
当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关;当
有关;当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关;当
有关;当![]() 时,认为事件
时,认为事件![]() 与
与![]() 是无关的)
是无关的)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD="40" m,则电视塔的高度为多少?
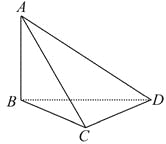
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com