Question

9．若实数x，y满足不等式$\left\{\begin{array}{l}{x+y≤3}\\{2x+y≥4}\\{x-2y≤2}\end{array}\right.$，且z=$\frac{y}{x}$，则z的取值范围是（　　）

• A． {z|0≤z≤$\frac{1}{8}$}
• B． {z|0≤z≤2}
• C． {z|z≤0或z≥$\frac{1}{8}$}
• D． {z|0z≤0或z≥2}

Answer 1

分析 作出题中不等式组表示的平面区域，得到如图的△ABC及其内部．设P（x，y）为区域内一点，定点Q（0，-1），可得目标函数z=$\frac{y}{x}$，表示P、Q两点连线的斜率，运动点P并观察直线PQ斜率的变化，即可得到z的最小值．

解答 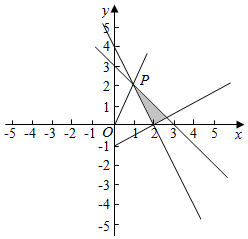解：作出不等式式$\left\{\begin{array}{l}{x+y≤3}\\{2x+y≥4}\\{x-2y≤2}\end{array}\right.$表示的平面区域，
得到如图的三角形及其内部，
其中P（1，2），设P（x，y）为区域内点，定点O（0，0）．
可得z=$\frac{y}{x}$表示P、O两点连线的斜率，
即z的最小值是0．
z的最大值为：$\frac{2}{1}$=2．
故选：B．

点评 本题给出二元一次不等式组，求目标函数z=$\frac{y}{x}$最值，着重考查了二元一次不等式组表示的平面区域和直线的斜率等知识，是中档题．