练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．已知i为虚数单位，复数z满足$\frac{1+z}{1-z}$=i，则z2016=（　　）
    A．-2iB．2iC．-1D．1

    分析 把已知等式变形得到$z=\frac{-1+i}{1+i}$，然后利用复数代数形式的乘除运算化简，再由虚数单位i的运算性质求得答案．

    解答 解：由$\frac{1+z}{1-z}$=i，得（1-z）i=1+z，即i-iz=1+z，
    ∴（1+i）z=-1+i，则$z=\frac{-1+i}{1+i}=\frac{（-1+i）（1-i）}{（1+i）（1-i）}=\frac{2i}{i}=i$，
    ∴z2016=i2016=（i2）1008=（-1）1008=1．
    故选：D．

    点评 本题考查复数代数形式的乘除运算，考查了虚数单位i得性质，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．在等差数列{an}中，已知an=11-2n，则使前n项和Sn最大的n值为（　　）
    A．4B．5C．6D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．在平面几何中，三角形的面积等于其周长的一半与其内切圆半径之积，类比之，在立体几何中，三棱锥的体积等于其表面积的$\frac{1}{3}$与其内切球半径之积（用文字表述）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．如果数据x1，x2，…，xn的平均数为2，方差为3，则数据3x1+5，3x2+5…，3xn+5的平均数和方差分别为（　　）
    A．11，25B．11，27C．8，27D．11，8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．如图，扇形OAB的中心角为直角，半径为1，点P为扇形OAB的弧$\widehat{AB}$上任意一点，设$\overrightarrow{OP}$=x$\overrightarrow{OB}$+y$\overrightarrow{OA}$（x，y∈R），$\overrightarrow a$=（x，y），$\overrightarrow b$=（${\sqrt{3}$，1），则$\overrightarrow a•\overrightarrow b$的最小值为（　　）
    A．-1B．-2C．1D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知集合A={1，2}，B={0，1}，则集合A∪B的所有子集的个数为8个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

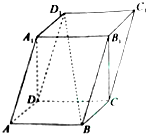    12．已知四棱柱ABCD-A1B1C1D1，侧面A1ADD1⊥面ABCD，底面ABCD是矩形，且AB=2，AD=1，AA1=$\sqrt{5}$，∠A1AD的余弦值为$\frac{\sqrt{5}}{5}$．
    （1）求证：平面A1DCB1⊥平面ABCD；
    （2）求BD1与平面ABCD所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．在数列{an}中，a1=1，a2=5，an+2=an+1-an（n∈N*），则a1000=-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．2016年里约奥运会和残奥会吉祥物的名字于2015年12月14日揭晓，两个吉祥物分别叫维尼修斯（Vinicius）和汤姆（Tom）（如图），以此纪念巴萨诺瓦曲风的著名音乐家Viniciusde Moraes和Tom Jobim．某商场在抽奖箱中放置了除图案外，其它无差别的8张卡片，其中2张印有“维尼修斯（Vinicius）”图案，n（2≤n≤4）张印有“汤姆（Tom）”图案，其余卡片上印有“2016年里约奥运会”的图案，
    （1）若n=4，从抽奖箱中任意取一卡片，记下图案后放回，连续抽取三次，求三次取出的卡片中，恰有两张印有“2016年里约奥运会”图片卡片的概率；
    （2）从抽奖箱中任意抽取两张卡片，两张卡片图案相同的概率是$\frac{2}{7}$．求n的值；
    （3）①当n=3时，随机抽取一次，若规定取出印有“维尼修斯（Vinicius）”图案的卡片获得16元购物券，取出印有“汤姆（Tom）”图案的卡片获得8元购物券，取出印有“2016年里约奥运会”的图案的卡片没有奖励，用ξ表示获得奖券的面值，求ξ的分布列和数学期望E（ξ）．
    ②在①的条件下，若商场每天有800人参与抽奖活动，顾客获得的购物券全部用于捆绑其他商品消费，每1元购物券能给商场带来10元纯利润，则商场每天在这个活动中能获得的纯利润是多少？

    查看答案和解析>>

    同步练习册答案