
| A. | y=cosx | B. | y=2|sinx| | C. | y=cos$\frac{x}{2}$ | D. | y=tanx |
分析 分别求出四个选项中函数的周期,排除选项后,再通过函数的单调减区间找出正确选项即可.
解答 解:由题意考察选项,可得
A、y=cosx的周期T=2π,不符合;
B、y=2|sinx|以π为最小正周期,且在区间($\frac{π}{2}$,π)上为减函数,正确;
C、y=cos$\frac{x}{2}$的最小正周期是4π,在区间($\frac{π}{2}$)上为减函数,不符合;
D、y=tanx的最小正周期是π,在区间($\frac{π}{2}$)上为增函数,不符合;
故选:B.
点评 本题是基础题,考查三角函数的周期,三角函数的单调性,计算能力体现学生的基本知识掌握的好坏,是常考题型.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
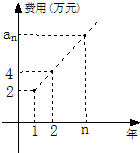 某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要支付设备的维修和工人工资等费用an的信息如图.
某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要支付设备的维修和工人工资等费用an的信息如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,都有x2=1 | B. | ?x0∉R,使得x2=1 | C. | ?x∈R,都有x2≠1 | D. | ?x0∈R,使得x2≠1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f (2014)>f (2015)>f (2016) | B. | f (2016)>f (2014)>f (2015) | ||
| C. | f (2016)=f (2014)>f (2015) | D. | f (2014)>f (2015)=f (2016) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com