
分析 (1)求出函数的导数,计算f′(0)=0,求出a的值,求出函数的单调区间即可;
(2)问题转化为ex-bx≥c,令g(x)=ex-bx,根据函数的单调性求出g(x)的最小值,得到b2c≤b3-b3lnb,令h(b)=b3-b3lnb,根据函数的单调性求出其最大值即可.
解答 解:(1)函数f(x)的定义域为(-∞,+∞),
因为f'(x)=ex+a,由已知得f'(0)=0,∴a=-1,
当x>0时,f'(x)=ex-1>0,当x<0时,f'(x)<0,
所以函数f(x)的单调递增区间为(0,+∞),单调递减区间为(-∞,0).
(2)不等式f(x)≥(b-1)x+c转化为ex-bx≥c,
令g(x)=ex-bx,g'(x)=ex-b,由g'(x)>0得,x>lnb,g'(x)<0得x<lnb,
所以函数g(x)在(-∞,lnb)上为减函数,在(lnb,+∞)上为增函数,
所以g(x)min=g(lnb)=b-blnb,∴c≤b-blnb,∴b2c≤b3-b3lnb,
令h(b)=b3-b3lnb,则h'(b)=b2(2-3lnb),
由h'(b)>0得$0<b<{e^{\frac{2}{3}}},h'(b)<0$得$b>{e^{\frac{2}{3}}}$,
所以函数h(b)在$({0,{e^{\frac{2}{3}}}})$上为增函数,在(${e}^{\frac{2}{3}}$,+∞)上为减函数,
所以h(b)的最大值为h(${e}^{\frac{2}{3}}$)=$\frac{1}{3}$e2,此时b=${e}^{\frac{2}{3}}$,
所以b2c的最大值为$\frac{1}{3}$${e}^{\frac{2}{3}}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 15° | B. | 75° | C. | 15°或75° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36种 | B. | 30种 | C. | 24种 | D. | 6种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知△ABC中,顶点A(7,-3),AC边上的高BH所在直线方程为x-2y-5=0,AB边上的中线CM所在的直线方程为6x-y-21=0.
已知△ABC中,顶点A(7,-3),AC边上的高BH所在直线方程为x-2y-5=0,AB边上的中线CM所在的直线方程为6x-y-21=0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
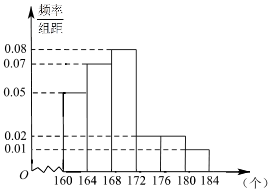 《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.
《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布N(168,16).现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组[160,164),第二组[164,168),…,第六组[180,184),如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,菱ABCD与四边形BDEF相交于BD,∠ABC=120°,BF⊥平面ABCD,DE∥BF,BF=2DE,AF⊥FC,M为CF的中点,AC∩BD=G.
如图,菱ABCD与四边形BDEF相交于BD,∠ABC=120°,BF⊥平面ABCD,DE∥BF,BF=2DE,AF⊥FC,M为CF的中点,AC∩BD=G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com