
【题目】已知函数f(x)= ![]()
(1)若对 ![]() ,f(x)
,f(x) ![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(2)已知常数a ![]() R,解关于x的不等式f(x)
R,解关于x的不等式f(x) ![]() .
.
【答案】
(1)解:由题意可知 ![]() >O,a≥
>O,a≥ ![]() 恒成立,即a≥(
恒成立,即a≥( ![]() )max;
)max;![]() , ∴a≥
, ∴a≥ ![]()
(2)解:①若a=O,则原不等式为-x≥0,故不等式的解集为{x|x≤0}.
②若a>0,△=1- 4a2
当 ![]() 时,即
时,即 ![]() 时,原不等式的解集为R.
时,原不等式的解集为R.
当 ![]() ,即
,即 ![]() 时,方程
时,方程 ![]() 的两根为
的两根为 ![]() ,
, ![]() ,
,
∴原不等式的解集为{x|x ![]() ,或x
,或x ![]() }.
}.
③若a<0,△=1-4 ![]() .
.
当 ![]() ,即
,即 ![]() ,原不等式的解集为{x|
,原不等式的解集为{x| ![]()
![]() x
x ![]() }.
}.
当 ![]() 时,
时, ![]() 时,原不等式化为
时,原不等式化为 ![]() ,
,
∴原不等式的解集为{x|x=1}.
当 ![]() ,即
,即 ![]() 时,原不等式的解集为
时,原不等式的解集为 ![]()
综上所述,当 ![]() 时,原不等式的解集为R;
时,原不等式的解集为R;
当 ![]() 时,原不等式的解集为{x|x
时,原不等式的解集为{x|x ![]() ,或x
,或x ![]() };
};
当a=0,原不等式为{x|x≤0}
当 ![]() 时,原不等式的解集为{x|
时,原不等式的解集为{x| ![]()
![]() x
x ![]() };
};
当a= ![]() 时,原不等式的解集为{x|x=1};
时,原不等式的解集为{x|x=1};
当a ![]() 时,原不等式的解集为
时,原不等式的解集为 ![]() .
.
【解析】(1)首先采用分离参变量的方法将a分离出来,转化为函数恒成立问题,再用均值不等式求分式的最大值,即可得到。
(2)根据二次函数的性质,对系数a和![]() 进行分类,a分为大于0,小于0,等于0三种情况,
进行分类,a分为大于0,小于0,等于0三种情况,![]() 分为大于0,小于等于0两种情况。然后将解得的范围整理即得。
分为大于0,小于等于0两种情况。然后将解得的范围整理即得。


科目:高中数学 来源: 题型:
【题目】已知以点![]() 为圆心的圆过点
为圆心的圆过点![]() 和
和![]() ,线段
,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,
,
(1)求直线![]() 的方程; (2)求圆
的方程; (2)求圆![]() 的方程。
的方程。
(3)设点![]() 在圆
在圆![]() 上,试探究使
上,试探究使![]() 的面积为 8 的点
的面积为 8 的点![]() 共有几个?证明你的结论
共有几个?证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理:“幂势既同,则积不容异”,它是中国古代一个涉及几何体体积问题,意思是两个等高的几何体,如在同高处的截面积恒相等,则体积相等,设A,B为两个等高的几何体,p:A,B的体积相等,q:A,B在同高处的截面积不恒相等,根据祖暅原理可知,q是-p的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为![]() 的函数
的函数![]() 满足:
满足:![]() ,且对于任意实数
,且对于任意实数![]() ,
,![]() 恒有
恒有![]() ,当
,当![]() 时,
时,![]() .
.
(1)求![]() 的值,并证明当
的值,并证明当![]() 时,
时,![]() ;
;
(2)判断函数![]() 在
在![]() 上的单调性并加以证明;
上的单调性并加以证明;
(3)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了数学测试,并从中随机抽取了60名学生的成绩(满分100分)作为样本,其中成绩不低于80分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.
(I)若该所中学共有3000名学生,试利用样本估计全校这次考试中优秀生人数;
(II)若在样本中,利用分层抽样的方法从成绩不低于70分的学生中随机抽取6人,再从中抽取3人,试求恰好抽中1名优秀生的概率.
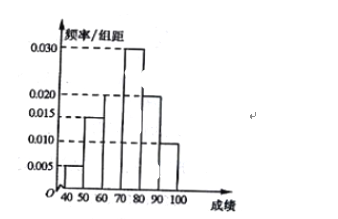
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且.
,且.![]() .
.
(1)求数列![]() 与
与![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项的
项的![]() ;
;
(3)将数列![]() 与
与![]() 的项相间排列构成新数列
的项相间排列构成新数列![]() ,设新数列
,设新数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数n都有
,若对任意正整数n都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com