
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
已知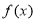 是定义在
是定义在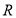 上的偶函数,且在区间
上的偶函数,且在区间 上单调递增,若实数
上单调递增,若实数 满足
满足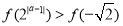 ,则
,则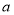 的取值范围是( )
的取值范围是( )
A.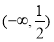 B.
B.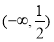

C.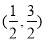 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
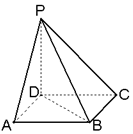 如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD.
如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
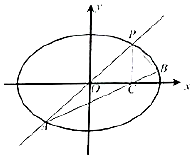 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )
如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )| A. | 168 | B. | 169 | C. | 170 | D. | 171 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com