
分析 设复数z1对应 $\overrightarrow{OA}$,z2对应 $\overrightarrow{OB}$,$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OC}$,判断三角形的性质.然后求解三角形即可.
解答  解:设复数z1对应 $\overrightarrow{OA}$,z2对应 $\overrightarrow{OB}$,$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OC}$,
解:设复数z1对应 $\overrightarrow{OA}$,z2对应 $\overrightarrow{OB}$,$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OC}$,
∵|z1|2+|z2|2 =($\sqrt{7}$+1)2+($\sqrt{7}$-1)2=16=42=|z1-z2|2,∴△AOB是直角三角形.
∴|z1+z2|=|z1-z2|=4.
故答案为:4.
点评 本题考查了复数的几何意义、三角形的解法、向量的运算,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 8π | C. | 4π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}π$ | B. | 6π | C. | $\frac{20π}{3}$ | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{16π}{3}$ | B. | $\frac{4π}{3}$ | C. | π | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
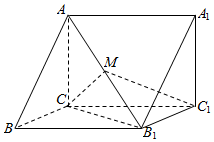 如图,在直三棱柱ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形.
如图,在直三棱柱ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日销售量 | [0,100] | [100,200] | [200,300] | [300,400] |
| 日销售量等级 | 差 | 中 | 良 | 优秀 |
| 天数 | 20 | 45 | 20 | 15 |
| 非优秀 | 优秀 | 总计 | |
| 夏季 | |||
| 非夏季 | |||
| 总计 | 100 |
| P(K2≥k0) | 0.1 | 0.05 | 0.025 | 0.01 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 405 | B. | 540 | C. | 810 | D. | 945 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com